Question

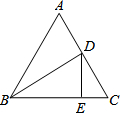
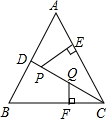
如图，△ABC中，AB=AC，∠A=∠ACB．
（1）求证：△ABC是等边三角形；
（2）若D为AB的中点，P为CD上的点，Q为PC的中点，且PE⊥AC于点E，QF⊥BC于点F，试求

4PE

QF

的立方根．

Answer 1

（1）证明：∵AB=AC，
∴∠ABC=∠ACB，
∵∠A=∠ACB，
∴∠A=∠ACB=∠ABC，
∴△ABC是等边三角形；

（2）∵D为AB的中点，
∴∠ACD=∠BCD=

1

2

×60°=30°，
∵PE⊥AC，QF⊥BC，
∴PE=

1

2

PC，QF=

1

2

CQ，
∵Q为PC的中点，
∴CQ=

1

2

PC，
∴PE=2QF，
∴

4PE

QF

=

4×2QF

QF

=8，
∴

4PE

QF

的立方根是2．