题目内容
 如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于E,则sinE的值为
如图,AB是⊙O的直径,C、D是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于E,则sinE的值为考点:切线的性质
专题:计算题
分析:连结OC,先根据圆周角定理得∠COB=2∠CDB=60°,再根据切线的性质得OC⊥CE,则∠OCE=90°,所以∠E=30°,然后根据特殊角的三角函数值求解.
解答: 解:连结OC,如图,
解:连结OC,如图,
∵∠CDB=30°,
∵∠COB=2∠CDB=60°,
∵CE为⊙O的切线,
∴OC⊥CE,
∴∠OCE=90°,
∴∠E=30°,
∴sinE=sin30°=
.
故答案为
.
 解:连结OC,如图,
解:连结OC,如图,∵∠CDB=30°,
∵∠COB=2∠CDB=60°,
∵CE为⊙O的切线,
∴OC⊥CE,
∴∠OCE=90°,
∴∠E=30°,
∴sinE=sin30°=
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理和特殊角的三角函数值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
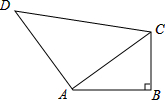 如图,∠B=90°,AB=4cm,BC=3cm,AD=12cm,CD=13cm,求四边形ABCD的面积.
如图,∠B=90°,AB=4cm,BC=3cm,AD=12cm,CD=13cm,求四边形ABCD的面积. 如图,已知直径为1个单位长度的圆形纸片上的点A与数轴上表示-1的点重合,若将该圆形纸片沿数轴顺时针滚动一周(无滑动)后点A与数轴上的点A′重合,则点A′表示的数为
如图,已知直径为1个单位长度的圆形纸片上的点A与数轴上表示-1的点重合,若将该圆形纸片沿数轴顺时针滚动一周(无滑动)后点A与数轴上的点A′重合,则点A′表示的数为 用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图的虚线处后绕点M逆时针方向旋转25°,则三角板的斜边与射线OA的夹角α为
用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图的虚线处后绕点M逆时针方向旋转25°,则三角板的斜边与射线OA的夹角α为