题目内容
7. 如图,在△ABC中,D是BC上的点,E是AC上的点,AD与BE相交于点F,若AE:EC=3:4,BD:DC=2:3,求BE:EF的值.
如图,在△ABC中,D是BC上的点,E是AC上的点,AD与BE相交于点F,若AE:EC=3:4,BD:DC=2:3,求BE:EF的值.
分析 过E作EG∥AD交BC于G.由EG∥AD,根据平行线分线段成比例定理得出$\frac{AE}{EC}$=$\frac{DG}{GC}$=$\frac{3}{4}$,于是GC=$\frac{4}{3}$DG,DC=DG+GC=$\frac{7}{3}$DG.再由$\frac{BD}{DC}$=$\frac{2}{3}$,得出BD=$\frac{2}{3}$DC=$\frac{14}{3}$DG,那么BG=BD+DG=$\frac{17}{3}$DG,然后由DF∥EG,根据平行线分线段成比例定理得出 $\frac{BE}{EF}$=$\frac{BE}{DG}$=$\frac{17}{3}$.
解答  解:过E作EG∥AD交BC于G.
解:过E作EG∥AD交BC于G.
∵EG∥AD,
∴$\frac{AE}{EC}$=$\frac{DG}{GC}$=$\frac{3}{4}$,
∴GC=$\frac{4}{3}$DG,
∴DC=DG+GC=$\frac{7}{3}$DG.
∵$\frac{BD}{DC}$=$\frac{2}{3}$,
∴BD=$\frac{2}{3}$DC=$\frac{14}{3}$DG,
∴BG=BD+DG=$\frac{17}{3}$DG,
又∵DF∥EG,
∴$\frac{BE}{EF}$=$\frac{BG}{DG}$=$\frac{17}{3}$.
点评 本题主要考查了平行线分线段成比例定理,用到的知识点:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例,准确作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.香蕉每千克m元,买10千克以上9折优惠(即按原价的90%出售),买20千克应付( )
| A. | 20m元 | B. | 20×90%m元 | C. | 20×(1+90%)m元 | D. | 20×(1-90%)m元 |
18.若a2=16,|b|=3,则a+b等于( )
| A. | -7 | B. | ±7 | C. | ±1 | D. | ±7或±1 |
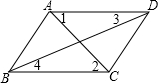 如图,在下列条件中:①∠1=∠2;②∠BAD=∠BCD;③∠3=∠4;④∠BAD+∠ABC=180°,能判定AB∥CD的有( )
如图,在下列条件中:①∠1=∠2;②∠BAD=∠BCD;③∠3=∠4;④∠BAD+∠ABC=180°,能判定AB∥CD的有( )