Question

【题目】如图，CB∥OA，∠C=∠OAB=124°，E、F在CB上，且满足∠FOB=∠AOB，OE平分∠COF，∠OEC=∠COB，则∠OEC=______.

Answer 1

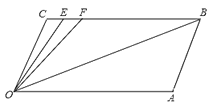
【答案】42°

【解析】

根据平行四边形的性质得∠OEC=∠EOB+∠AOB，∠OBA=∠BOC=∠COE+∠EOB，再根据CO∥AB，∠OEC=∠COB得∠OEC=∠COB=∠OBA，求出∠COE和∠EOB即可得出答案.

解：∵CB∥OA，∠C=∠OAB=124°，

∴∠AOC=∠ABC=56°，

则四边形AOCB为平行四边形，

则∠OEC=∠EOB+∠AOB，∠OBA=∠BOC=∠COE+∠EOB，

又∵CO∥AB，∠OEC=∠COB，

∴∠OEC=∠COB=∠OBA，

则∠AOB=∠COE，

则∠COE=∠EOF=∠FOB=∠AOB=56°÷4=14°，

则∠EOB=2×14°=28°，

此时∠OBA=∠OEC=28°+14°=42°．