Question

我们把正六边形的顶点及其对称中心称作如图1所示基本图的特征点，显然这样的基本图共有7个特征点，将此基本图不断复制并平移，使得相邻两个基本图的一边重合，这样得到图2，图3，…

（1）观察以上图形并完成下表：

图形的名称	基本图的个数	特征点的个数
图1	1	7
图2	2	12
图3	3	17
图4	4	______
…	…	…

猜想：在图（n）中，特征点的个数为______（用n表示）；
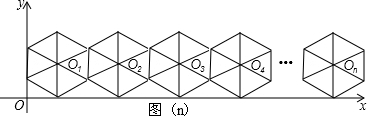
（2）如图，将图（n）放在直角坐标系中，设其中第一个基本图的对称中心O₁的坐标为（x₁，2），则x₁=______

Answer 1

【答案】分析：（1）观察图形，结合已知条件，得出将基本图每复制并平移一次，特征点增加5个，由此得出图4中特征点的个数为17+5=22个，进一步猜想出：在图（n）中，特征点的个数为：7+5（n-1）=5n+2；
（2）过点O₁作O₁M⊥y轴于点M，根据正六边形、等腰三角形的性质得出∠BO₁M=30°，再由余弦函数的定义求出O₁M=，即x₁=；然后结合图形分别得出图（2）、图（3）、图（4）的对称中心的横坐标，找到规律，进而得出图（2013）的对称中心的横坐标．
解答：解：（1）由题意，可知图1中特征点有7个；
图2中特征点有12个，12=7+5×1；
图3中特征点有17个，17=7+5×2；
所以图4中特征点有7+5×3=22个；
由以上猜想：在图（n）中，特征点的个数为：7+5（n-1）=5n+2；

（2）如图，过点O₁作O₁M⊥y轴于点M，
又∵正六边形的中心角=60°，O₁C=O₁B=O₁A=2，
∴∠BO₁M=30°，
∴O₁M=O₁B•cos∠BO₁M=2×=，
∴x₁=；
由题意，可得图（2）的对称中心的横坐标为（2×2）=2，
图（3）的对称中心的横坐标为（2×3）=3，
图（4）的对称中心的横坐标为（2×4）=4，
…
∴图（2013）的对称中心的横坐标为（2×2013）=2013．
故答案为22，5n+2；，2013．
点评：本题借助正六边形考查了规律型：图形的变化类问题，难度适中．关键是通过观察、归纳与总结，得到其中的规律；（2）要注意求的是整个图形的对称中心的横坐标，而不是第2013个正六边形的对称中心的横坐标，这也是本题容易出错的地方．