Question

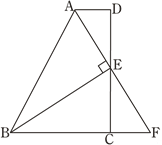
【题目】如图，已知∠MON＝30°，点 A1,A2,A3…在射线ON 上，点B1,B2,B3…在射线OM 上，△A1B1A2，△A2B3A3，△A3B3A4 均为等边三角形，若OA1=2，则△A7B7A8 的边长为____.

Answer 1

【答案】128

【解析】

先根据等边三角形的各边相等且各角为60°得：∠B1A1A2=60°，A1B1=A1A2，再利用外角定理求∠OB1A1=30°，则∠MON=∠OB1A1，由等角对等边得：B1A1=OA1=2，得出△A1B1A2的边长为2，再依次同理得出：△A2B2A3的边长为4，△A4B4A5的边长为：24=16，则△A5B5A6的边长为：25=32，同理可得△A7B7A8 的边长为27.

∵△A1B1A2为等边三角形，

∴∠B1A1A2=60°，A1B1=A1A2，

∵∠MON=30°，

∴∠OB1A1=60°-30°=30°，

∴∠MON=∠OB1A1，

∴B1A1=OA1=2，

∴△A1B1A2的边长为2，

同理得：∠OB2A2=30°，

∴OA2=A2B2=OA1+A1A2=2+2=4，

∴△A2B2A3的边长为4，

同理可得：、△A3B3A4的边长为：23=8，

△A4B4A5的边长为：24=16，

△A5B5A6的边长为：25=32，

△A6B6A7的边长为：26=64，

△A7B7A8的边长为：27=128.

故答案为：128.