Question

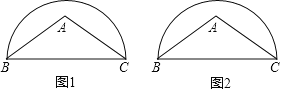
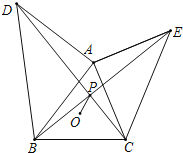
【题目】如图，已知△ABC，外心为O，BC＝10，∠BAC＝60°，分别以AB，AC为腰向形外作等腰直角三角形△ABD与△ACE，连接BE，CD交于点P，则OP的最小值是_____．

Answer 1

【答案】5﹣．

【解析】

根据已知条件证明△DAC≌△BAE，得到∠DPB=90°，证明点P在以BC为直径的圆上，再在△BOC中，求出OH的长，得到答案．

解：如图，

∵∠BAD＝∠CAE＝90°，

∴∠DAC＝∠BAE，

在△DAC和△BAE中，

，

∴△DAC≌△BAE（SAS），

∴∠ADC＝∠ABE，

∴∠PDB+∠PBD＝90°，

∴∠DPB＝90°，

∴点P在以BC为直径的圆上，

∵外心为O，∠BAC＝60°，

∴∠BOC＝120°，又BC＝10，

∴OH＝，

所以OP的最小值是：．