题目内容
如图，Rt△ABC中，∠C=90°，AC=6，CB=8，则△ABC的内切圆半径r为（ ）| A、1 | B、2 | C、1.5 | D、2.5 |
考点：三角形的内切圆与内心
专题：计算题
分析：先根据勾股定理计算出AB，然后利用直角边为a、b，斜边为c的三角形的内切圆半径为
进行计算．
| a+b-c |
| 2 |
解答：解：∵∠C=90°，AC=6，CB=8，
∴AB=
=10，
∴△ABC的内切圆半径r=
=2．
故选B．
∴AB=
| AC2+BC2 |
∴△ABC的内切圆半径r=
| 6+8-10 |
| 2 |
故选B．
点评：本题考查了三角形的内切圆与内心：与三角形各边都相切的圆叫三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．三角形的内心就是三角形三个内角角平分线的交点．记住直角边为a、b，斜边为c的三角形的内切圆半径为
．
| a+b-c |
| 2 |
练习册系列答案
相关题目
如图，正六边形ABCDEF内接于⊙O，若⊙O的内接正△ACE的面积为48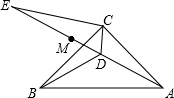
如图，在△ABC中，AC=BC，∠ACB=90°，点D为△ABC内一点，∠CAD=∠CBD=15°，E为AD延长线上的一点，且CE=CA．
二次函数y=ax2+bx+c的图象如图所示，下列结论错误的是（ ）| A、a＜0 |
| B、c＞0 |
| C、b2-4ac＞0 |
| D、当x＜2时，函数值y随x增大而增大；当x＞2时，函数值y随x增大而减小 |
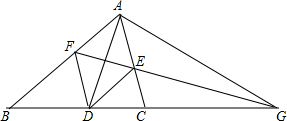如图，AD是∠BAC的平分线，DE平行AB交AC于点E，DF平行AC交AB于点F，延长FE交BC的延长线于点G，求证：