题目内容
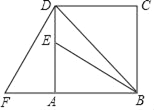
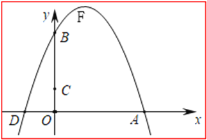
【题目】抛物线![]() 与y轴交于B,与x轴交于点D、A,点A在点D的右边,顶点为F,
与y轴交于B,与x轴交于点D、A,点A在点D的右边,顶点为F,![]()
(1)直接写出点B、A、F的坐标;
(2)设Q在该抛物线上,且![]() ,求点Q的坐标;
,求点Q的坐标;
(3)对大于1常数m,在x轴上是否存在点M,使得![]() ?若存在,求出点M坐标;若不存在,说明理由?
?若存在,求出点M坐标;若不存在,说明理由?
【答案】(1)A(3,0)B(0,3),F(1,4);(2)点Q(2,3)或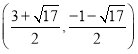 或
或 ;(3)
;(3)![]() 或
或![]()
【解析】
(1)![]() ,令
,令![]() ,解得:
,解得:![]() 或
或![]() ,即可求解;
,即可求解;
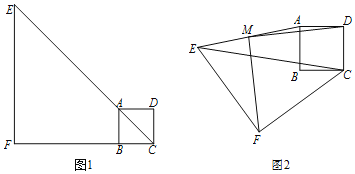
(2)连接AB,过点F作直线m平行于直线AB交抛物线与点Q,在BA下方作直线n,使直线m、n与直线AB等距离,过点F作x轴的垂线交AB于点H、交直线n与点![]() ,直线n与抛物线交于点
,直线n与抛物线交于点![]() 、
、![]() ,即可求解;
,即可求解;
(3)由![]() ,则
,则![]() ,
, ,即可求解.
,即可求解.
(1)![]() ,
,
令![]() ,解得:
,解得:![]() 或
或![]() ,
,
令![]() ,则
,则![]() ,故点
,故点![]() ,
,
同理点![]() ;
;
(2)连接AB,过点F作直线m平行于直线AB交抛物线与点Q,在BA下方作直线n,使直线m、n与直线AB等距离,
过点F作x轴的垂线交AB于点H、交直线n与点![]() ,直线n与抛物线交于点
,直线n与抛物线交于点![]() 、
、![]() ,
,

直线BA的表达式为:![]() ,
,
则直线m的表达式为:![]() ,将点F坐标代入上式并解得:
,将点F坐标代入上式并解得:
直线m的表达式为:![]() ,
,
联立![]() 并解得:
并解得:![]() 或
或![]() 舍去
舍去![]() ,
,
故点![]() ;
;
则点![]() ,则
,则![]() ,
,
故直线n的表达式为:![]() ,
,
联立![]() 并解得:
并解得:![]() ,
,
故点Q坐标为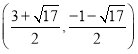 或
或 ,
,
综上,点![]() 或
或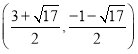 或
或 ;
;
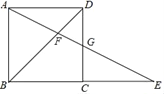
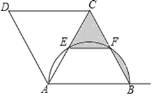
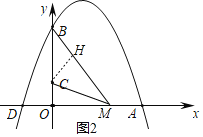
(3)过点C作![]() 于点H,
于点H,
设:![]() ,则
,则![]() ,
,![]() ,
,
![]() ,则
,则![]() ,
,
 ,
,
解得:![]() ,
,
即点![]() 或
或![]() .
.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目