Question

【题目】在平面直角坐标系中（如图），已知二次函数（其中a、b、c是常数，且a≠0）的图像经过点A（0，-3）、B（1，0）、C（3，0），联结AB、AC．

（1）求这个二次函数的解析式；

（2）点D是线段AC上的一点，联结BD，如果，求tan∠DBC的值；

（3）如果点E在该二次函数图像的对称轴上，当AC平分∠BAE时，求点E的坐标．

Answer 1

【答案】（1）；（2）；（3）E（2，）

【解析】

（1）直接利用待定系数法，把A、B、C三点代入解析式，即可得到答案；

（2）过点D作DH⊥BC于H，在△ABC中，设AC边上的高为h，利用面积的比得到，然后求出DH和BH，即可得到答案；

（3）延长AE至x轴，与x轴交于点F，先证明△OAB∽△OFA，求出点F的坐标，然后求出直线AF的方程，即可求出点E的坐标.

解：（1）将A（0，-3）、B（1，0）、C（3，0）代入得，

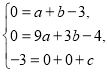
解得，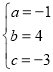

∴此抛物线的表达式是：．

（2）过点D作DH⊥BC于H，

在△ABC中，设AC边上的高为h，则，

又∵DH//y轴，

∴．

∵OA=OC=3，则∠ACO=45°，

∴△CDH为等腰直角三角形，

∴．

∴．

∴tan∠DBC=.

（3）延长AE至x轴，与x轴交于点F，

∵OA=OC=3，

∴∠OAC=∠OCA=45°，

∵∠OAB=∠OAC∠BAC=45°∠BAC，∠OFA=∠OCA∠FAC=45°∠FAC，

∵∠BAC=∠FAC，

∴∠OAB=∠OFA．

∴△OAB∽△OFA，

∴．

∴OF=9，即F（9，0）；

设直线AF的解析式为y=kx+b（k≠0），

可得 ，解得，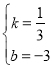

∴直线AF的解析式为：，

将x=2代入直线AF的解析式得：，

∴E（2，）.