题目内容
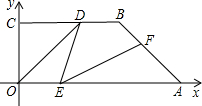
 如图,OA是⊙O的半径,延长OA至B,使OA=AB,C是OA的中点,D是圆周上的点,连接CD、BD
如图,OA是⊙O的半径,延长OA至B,使OA=AB,C是OA的中点,D是圆周上的点,连接CD、BD
求证:BD=2CD.
 证明:连接OD,如右图所示,
证明:连接OD,如右图所示,∵C是OA中点,
∴OC=
 OA,
OA,∴OC=
 OD,
OD,又∵A是OB中点,
∴OA=
 OB,
OB,∴OD=
 OB,
OB,∴
 =
= =
= ,
,∠COD=∠DOB,
∴△COD∽△DOB,
∴
 =
= ,
,∴BD=2CD.
分析:先连接OD,利用中点定义易证
 =
= =
= ,而∠COD=∠DOB,从而可证△COD∽△DOB,再利用相似三角形的性质可求
,而∠COD=∠DOB,从而可证△COD∽△DOB,再利用相似三角形的性质可求 =
= ,即BD=2CDE.
,即BD=2CDE.点评:本题考查了中点定义、相似三角形的判定和性质.关键是证明△COD∽△DOB(如果两条边对应成比例且夹角相等的两个三角形相似).

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

 上的点E处.
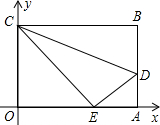
上的点E处. 如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在X轴,y轴的正半轴上.OA∥BC,D是BC上一点,BD=
如图,直角梯形OABC的直角顶点是坐标原点,边OA,OC分别在X轴,y轴的正半轴上.OA∥BC,D是BC上一点,BD= 如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.
如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.