题目内容
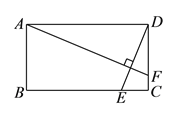
【题目】如图,矩形![]() 中,
中, ![]() ,
, ![]() ,动点
,动点![]() 在边
在边![]() 上,连结
上,连结![]() ,过点
,过点![]() 作
作![]() 的垂线
的垂线![]() ,交直线
,交直线![]() 于点
于点![]() .设
.设![]() ,
, ![]() .
.
(![]() )求
)求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(![]() )当
)当![]() 时,求
时,求![]() 的长.
的长.
(![]() )若直线
)若直线![]() 与线段
与线段![]() 延长线交于点
延长线交于点![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)易证△ADF∽△DCE,然后运用相似三角形的性质即可得到y与x的关系,然后根据y的范围就可得到x的范围;
(2)由于点F的位置不确定,需分点F在线段DC及点F在线段DC的延长线上两种情况进行讨论,然后利用y与x的关系即可解决问题;
(3)由∠DEC=∠AFD=90-∠EDC可得∠BED=∠DFG,因而在△DBE和△DFG中,点E与点F是对应点,故当△DBE与△DFG相似时,可分△DEB∽△GFD和△DEB∽△DFG两种情况进行讨论,然后只需用x的代数式表示ED、FG、EB,再运用相似三角形的性质即可解决问题.
试题解析:解:(![]() )在矩形
)在矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .
.
又∵![]() ,∴
,∴![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() ,∴
,∴![]() 即
即![]() ,∴
,∴![]() .
.
又点![]() 在边
在边![]() 上,∴
上,∴![]() ,∴
,∴![]() .
.
(![]() )当
)当![]() 时,
时,
①当![]() 在线段
在线段![]() 上时,
上时, ![]() ,此时
,此时![]() .
.
②当![]() 在线段
在线段![]() 延长线上时,
延长线上时, ![]() ,
, ![]() .
.
∴综上, ![]() 时 ,
时 , ![]() 长为
长为![]() 或
或![]() .
.
(![]() )在
)在![]() 中,
中, ![]() .
.
在![]() 中,
中, ![]() .
.
∵![]() 是矩形,∴
是矩形,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴ .
.
当![]() 时,
时, ![]() ,即
,即 ,
,
∴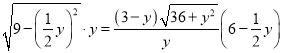 ,
,
解方程可得![]() ,∴
,∴![]() 的长为
的长为![]() .
.


练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目






