题目内容
两条平行线被第三条直线所截,同旁内角的平分线( )
| A、平行 | B、垂直 |
| C、相交 | D、无法判断 |
考点:平行线的性质
专题:
分析:根据两直线平行,同旁内角互补可得它们的度数之和是180°,再根据角平分线的定义求出它们一半的度数之和是90°,然后利用三角形的内角和等于180°求出两角平分线的夹角是90°,从而得解.
解答: 解:两平行线被第三条直线所截,同旁内角的平分线互相垂直,理由为:
解:两平行线被第三条直线所截,同旁内角的平分线互相垂直,理由为:
证明:如图,∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵AE平分∠BAC,CE平分∠ACD,
∴∠CAE=
∠BAC,∠ACE=
∠ACD,
∴∠CAE+∠ACE=
(∠BAC+∠ACD)=
×180°=90°,
在△ACE中,∠E=180°-(∠CAE+∠ACE)=180°-90°=90°,
∴两平行线被第三条直线所截,同旁内角的平分线互相垂直,
故选B.
 解:两平行线被第三条直线所截,同旁内角的平分线互相垂直,理由为:
解:两平行线被第三条直线所截,同旁内角的平分线互相垂直,理由为:证明:如图,∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵AE平分∠BAC,CE平分∠ACD,
∴∠CAE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CAE+∠ACE=
| 1 |
| 2 |
| 1 |
| 2 |
在△ACE中,∠E=180°-(∠CAE+∠ACE)=180°-90°=90°,
∴两平行线被第三条直线所截,同旁内角的平分线互相垂直,
故选B.
点评:本题考查了平行线的性质,角平分线的定义,以及三角形的内角和定理,作出图形更形象直观,且有助于问题的理解.

练习册系列答案
相关题目
计算5
-
+
的结果估计在( )
|
| 5 |
| 2 |
|
| 20 |
| A、3至4之间 |
| B、4至5之间 |
| C、5至6之间 |
| D、6至7之间 |
下列说法错误的是( )
A、±
| ||
B、±
| ||
| C、3是9的一个平方根 | ||
| D、0没有平方根 |
已知一个二元一次方程的一个解是
,则这个方程可能是( )
|
| A、x+y=3 | B、x+y=0 |
| C、x-y=3 | D、x=2y |
小明想做一个直角三角形的木架,下列四组长度的木棒中哪一组能刚好做成( )
| A、2、3、4 |
| B、6、7、8 |
| C、5、12、13 |
| D、6、8、12 |
如果x=3m+1,y=2+9m,那么用x的代数式表示y为( )
| A、y=2x |
| B、y=x2 |
| C、y=(x-1)2+2 |
| D、y=x2+1 |
为了解某县八年级学生的身高情况,从该县八年级学生中抽取了600名学生进行调查,下列说法中不正确的是( )
| A、以上调查方式属于抽样调查 |
| B、所抽取的600名学生是总体的一个样本 |
| C、总体是该县八年级学生身高的全体 |
| D、样本容量是600 |
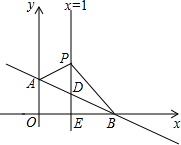 如图,平面直角坐标系中,直线AB:
如图,平面直角坐标系中,直线AB: