题目内容
如图，函数y=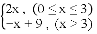
的图象与双曲线y=
(k≠0，x>0)相交于点A(3，m)和点B．
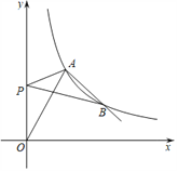
（1）求双曲线的解析式及点B的坐标；
（2）若点P在y轴上，连接PA，PB，求当PA+PB的值最小时点P的坐标．
练习册系列答案
一课一练课时达标系列答案
相关题目
一课一练课时达标系列答案题目内容
如图，函数y=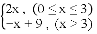的图象与双曲线y=(k≠0，x>0)相交于点A(3，m)和点B．
（1）求双曲线的解析式及点B的坐标；
（2）若点P在y轴上，连接PA，PB，求当PA+PB的值最小时点P的坐标．
一课一练课时达标系列答案
|+（π﹣2017）0﹣2sin30°+3﹣1．
与y=ax+1（a≠0）的图象可能是（ ）
B．
C．
D．
﹣7
= ．
有意义，则实数a的取值范围是（ ）
(m<0)图象上的两点,则y1____y2(填“>”“=”或“<”)
x （0＜x＜50），搭配一个B种造型的成本为80元．现在观海大道两侧也需搭配A、B两种园艺造型共50个，要求每种园艺造型不得少于20个，并且成本总额y（元）控制在4500元以内. 以上要求能否同时满足？请你通过计算说明理由.