题目内容
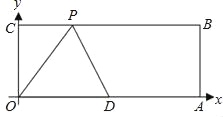
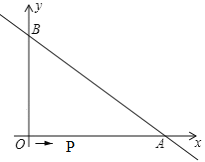
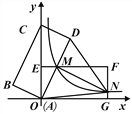
【题目】如图,矩形ABCD的顶点A在坐标原点,顶点C在y轴上,OB=2![]() 。将矩形ABCD绕点O顺时针旋转60°,使点D落在x轴的点G处,得到矩形AEFG,EF与AD交于点M,过点M的反比例函数图象交FG于点N,连接DN.
。将矩形ABCD绕点O顺时针旋转60°,使点D落在x轴的点G处,得到矩形AEFG,EF与AD交于点M,过点M的反比例函数图象交FG于点N,连接DN.
(1)求反比例函数的解析式
(2)求△AMN的面积;
【答案】(1)![]() (2)
(2)![]()
【解析】分析:(1)由旋转的性质得OB=OE=2![]() , ∠DOG=60,解Rt△EOM,求出EM的长,从而可得点M的坐标,然后用待定系数法求过点M的反比例函数解析式;
, ∠DOG=60,解Rt△EOM,求出EM的长,从而可得点M的坐标,然后用待定系数法求过点M的反比例函数解析式;
(2)根据![]() 计算即可.
计算即可.
详解:(1) 由题意可得:![]() °
°
∴![]() °
°![]() °
°![]() °
°
在![]() 中,
中,![]()
∴![]()
∴反比例函数解析式为:![]()

(2) 在![]() 中,
中,![]() °,
°,
∴![]() ,
,
∴![]()
∴![]() .
.
在![]() 中,当
中,当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() .
.
由(1)可知:![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]()
![]() .
.

练习册系列答案
相关题目
【题目】为转变教育管理方式并为学校教育教学提供参考,某区240名学生参加2019年国家义务教育质量检测,在测试中随机抽取若干名学生的音乐成绩进行
某区音乐成绩分布表
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
某区音乐成绩频数分布直方图
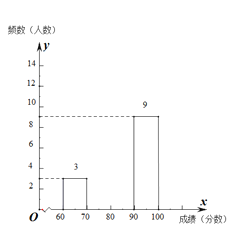
(1)频数分布表中:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)根据题意,补全频数分布直方图;
(3)如果成绩达到90及90分以上者为优秀,估计该区优秀学生大约有![]() 人.
人.