Question

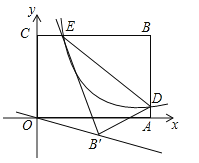
【题目】如图，平面直角坐标系xOy中，矩形OABC的边OA、OC分别落在x、y轴上，点B坐标为（6，4），反比例函数的图象与AB边交于点D，与BC边交于点E，连结DE，将△BDE沿DE翻折至△B'DE处，点B'恰好落在正比例函数y=kx图象上，则k的值是（ ）

A． B． C． D．

Answer 1

【答案】B．

【解析】

试题分析：∵矩形OABC，∴CB∥x轴，AB∥y轴，∵点B坐标为（6，4），∴D的横坐标为6，E的纵坐标为4，∵D，E在反比例函数的图象上，∴D（6，1），E（，4），∴BE=6﹣=，BD=4﹣1=3，∴ED==，连接BB′，交ED于F，过B′作B′G⊥BC于G，∵B，B′关于ED对称，∴BF=B′F，BB′⊥ED，∴BFED=BEBD，即BF=3×，∴BF=，∴BB′=，设EG=x，则BG=﹣x，∵BB′2﹣BG2=B′G2=EB′2﹣GE2，∴，∴x=，∴EG=，∴CG=，∴B′G=，∴B′（，﹣），∴k=．故选B．