题目内容
【题目】如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.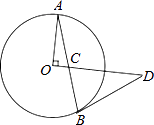
(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.
【答案】
(1)证明:连接OB,

∵OA=OB,DC=DB,
∴∠A=∠ABO,∠DCB=∠DBC,
∵AO⊥OD,
∴∠AOC=90°,即∠A+∠ACO=90°,
∵∠ACO=∠DCB=∠DBC,
∴∠ABO+∠DBC=90°,即OB⊥BD,
则BD为圆O的切线
(2)解:设BD=x,则OD=x+1,而OB=OA=3,
在Rt△OBD中,OB2+BD2=OD2,
即32+x2=(x+1)2,,
解得x=4,
∴线段BD的长是4.
【解析】(1)要证明BD为圆O的切线,连半径OB,需证OB⊥BD。由已知OA=OB,DC=DB,AO⊥OD,可以得出∠ACO=∠DCB=∠DBC,,即可求证结论。
(2)设BD=x,表示出OD的长,在在Rt△OBD中,根据勾股定理,建立方程,求解即可得到BD的长。
【考点精析】本题主要考查了等腰三角形的性质和勾股定理的概念的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】甲、乙两名选手在同等条件下进行射击对抗赛,他们各射靶10次,为了比较两人的成绩,制作了如下统计图表:
甲、乙射击成绩统计表
平均数 | 众数 | 中位数 | 方差 | 10环次数 | |
甲 | 8 | ||||
乙 |

(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?