题目内容
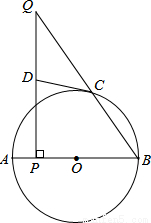
如图,AB为的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q。
(1)在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由。

(2)若cosB=![]() ,BP=6,AP=1,求QC的长。
,BP=6,AP=1,求QC的长。
解析】解:(1)CD是⊙O的切线,
理由如下:连接OC,∵OC=OB,∴∠B=∠1.又∵DC=DQ,∴∠Q=∠2
∵PQ⊥AB,∴∠QPB=90°∴∠B+∠Q=90°∴∠1+∠2=90°∴∠DCO=∠QCB-(∠1+∠2)=180°-90°,
∴OC⊥DC,∵OC是⊙O的半径∴CD是⊙O的切线
(2)连接AC,∵AB是⊙O的直径,∴∠ACB=90°.
在Rt△ABC中,

BC=ABcosB=(AP+BP) cosB=(1+6)×![]() =
=![]() .
.
在Rt△BPQ中BQ=![]() =
=![]() =10
=10
∴QC=BQ-BC=10=![]() =
=![]()

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
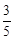 ,BP=6,AP=1,求QC的长。
,BP=6,AP=1,求QC的长。 的直径,CD为
的直径,CD为
 的直径,CD为
的直径,CD为
 的直径,CD为
的直径,CD为