Question

△ABC中，AE平分∠BAC，∠C＞∠B．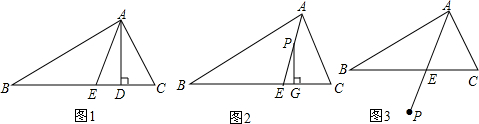
（1）①在图1中，若AD⊥BC于D，∠C=60°、∠B=40°则∠DAE=

 

；
②在图2中，若点P是AE上的一动点，过点P作PG⊥BC于G，则∠EPG与∠C、∠B之间的相等关系是

 

；
（2）若点P是AE延长线上一点，过点P作PG⊥BC于G，则∠EPG与∠C、∠B之间有何相等关系？画出图并证明你的结论．

Answer 1

考点：三角形内角和定理,三角形的外角性质

专题：探究型

分析：（1）①先求出∠BAC，根据角平分线定义求出∠CAE，根据三角形内角和定理求出∠CAD，代入∠DAE=∠CAE-∠CAD求出即可；
②先求出∠EFG=∠DAE，求出∠BAC，根据角平分线定义求出∠CAE，根据三角形内角和定理求出∠CAD，代入∠DAE=∠CAE-∠CAD求出∠DAE即可；
（2）先求出∠EFG=∠DAE，求出∠BAC，根据角平分线定义求出∠CAE，根据三角形内角和定理求出∠CAD，代入∠DAE=∠CAE-∠CAD求出∠DAE即可；

解答：解：
（1）①如图1，∵∠C=60°、∠B=40°，
∴∠CAB=180°-（∠B+∠C）=80°，
∵AE平分∠BAC，
∴∠EAC=

1

2

∠BAC=

1

2

×80°=40°，
∵AD⊥BC，
∴∠ADC=90°，
∵∠C=60°，
∴∠DAC=180°-90°-60°=30°，
∴∠DAE=∠CAE-∠CAD=40°-30°=10°，
故答案为：10°；

②∠EPG=

1

2

∠C-

1

2

∠B，
理由是：如图2，过A作AD⊥BC于D，
∵PG⊥BC，
∴AD∥PG，
∴∠DAE=∠GPE，
∵∠CAB=180°-（∠B+∠C），
∵AE平分∠BAC，
∴∠EAC=

1

2

∠BAC=

1

2

[180°-（∠B+∠C）]=90°-

1

2

∠B-

1

2

∠C，
∵AD⊥BC，
∴∠ADC=90°，
∴∠DAC=90°-∠C，
∴∠DAE=∠CAE-∠CAD=90°-

1

2

∠B-

1

2

∠C-（90°-∠C）=

1

2

∠C-

1

2

∠B，
∴∠EPG=

1

2

∠C-

1

2

∠B，
故答案为：∠EPG=

1

2

∠C-

1

2

∠B；

（2）∠EG=

1

2

∠C-

1

2

∠B，
证明：如图3，过A作AD⊥BC于D，
∵PG⊥BC，
∴AD∥PG，
∴∠DAE=∠GPE，
∵∠CAB=180°-（∠B+∠C），
∵AE平分∠BAC，
∴∠EAC=

1

2

∠BAC=

1

2

[180°-（∠B+∠C）]=90°-

1

2

∠B-

1

2

∠C，
∵AD⊥BC，
∴∠ADC=90°，
∴∠DAC=90°-∠C，
∴∠DAE=∠CAE-∠CAD=90°-

1

2

∠B-

1

2

∠C-（90°-∠C）=

1

2

∠C-

1

2

∠B，
∴∠EPG=

1

2

∠C-

1

2

∠B．

点评：本题考查了三角形的内角和定理，角平分线定义，平行线的性质和判定的应用，主要考查学生运用定理进行推理的能力，题目比较好，证明过程类似．