题目内容
如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C).若线段AD长为正整数,则点D的个数共有( )
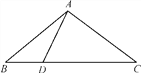
A. 5个 B. 4个 C. 3个 D. 2个
练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
题目内容
如图,在△ABC中,AB=AC=5,BC=8,D是线段BC上的动点(不含端点B,C).若线段AD长为正整数,则点D的个数共有( )

A. 5个 B. 4个 C. 3个 D. 2个
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案