题目内容
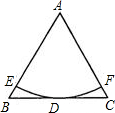如图，正△ABC的边长AB=2，以A为圆心的圆切BC于点D，交AB于点E，交AC于点F，则弧EF的长=分析：连AD，由BC为⊙O的切线，得到AD⊥BC，则AD为正△ABC的高，所以AD=
AB，而AB=2，可得到AD=
，又∠BAC=60°，然后利用弧长公式即可计算出弧EF的长．
| ||
| 2 |
| 3 |
解答：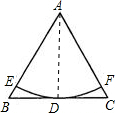
解：连AD，如图，
∵BC为⊙O的切线，
∴AD⊥BC，
而△ABC为正三角形，AB=2，
∴AD=
AB=
，∠BAC=60°，
∴弧EF的长=
=
．
故答案为
．
解：连AD，如图，∵BC为⊙O的切线，
∴AD⊥BC，
而△ABC为正三角形，AB=2，
∴AD=
| ||
| 2 |
| 3 |
∴弧EF的长=
60×π×
| ||
| 180 |
| ||
| 3 |
故答案为
| ||
| 3 |
点评：本题考查了弧长的计算公式：l=
，其中l表示弧长，n表示弧所对的圆心角的度数．
| nπR |
| 180 |
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
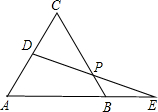交BC于点P．
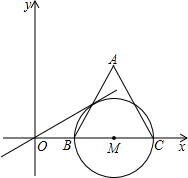点，以BC为直径的⊙M交AB于E．
如图，正△ABC的边长为3，绕其中心O将△ABC旋转180°得到△DEF，则△ABC和△DEF重叠部分的面积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、6
|
（2012•内江）如图，正△ABC的边长为3cm，动点P从点A出发，以每秒1cm的速度，沿A→B→C的方向运动，到达点C时停止，设运动时间为x（秒），y=PC2，则y关于x的函数的图象大致为（ ）