题目内容
等腰直角△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O与直线AB的距离为5.现两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,同时△ABC的边长AB、BC又以每秒0.5个单位沿BA、BC方向增大.

(1)△ABC的边与圆第一次相切时,点B运动了多少距离?
(2)从△ABC的边与圆第一次相切到最后一次相切,共经过多少时间?
(3)是否存在某一时刻,△ABC与⊙O的公共部分等于⊙O的面积?若存在,求出恰好符合条件时两个图形各运动了多少时间;若不存在,请说明理由.

(1)△ABC的边与圆第一次相切时,点B运动了多少距离?
(2)从△ABC的边与圆第一次相切到最后一次相切,共经过多少时间?
(3)是否存在某一时刻,△ABC与⊙O的公共部分等于⊙O的面积?若存在,求出恰好符合条件时两个图形各运动了多少时间;若不存在,请说明理由.
分析:(1)当△ABC第一次与圆相切时,应是AC与圆相切.如图,△ABC移至△A′B′C′处,A′C′与⊙O切于点E,连OE并延长,交B′C′于F.设⊙O与直线l切于点D,连OD,则OE⊥A′C′,OD⊥直线l.由切线长定理,以及直角三角形的性质可求得CD的值,进而求得CC′的值,从而求得点C运动的时间,也就有了点运动的时间,点B移动的距离可求得;
(2)△ABC与⊙O从开始运动到最后一次相切时,应为AB与圆相切,路程差为6,速度差为1,故从开始运动到最后一次相切的时间为6秒.
(3)若圆能在△ABC的内部时,则存在;若圆O不能在三角形的内部,则不存在;即求在(2)条件下,AC与圆的位置关系即可.
(2)△ABC与⊙O从开始运动到最后一次相切时,应为AB与圆相切,路程差为6,速度差为1,故从开始运动到最后一次相切的时间为6秒.
(3)若圆能在△ABC的内部时,则存在;若圆O不能在三角形的内部,则不存在;即求在(2)条件下,AC与圆的位置关系即可.
解答:解:(1)设第一次相切时,△ABC移至△A′B′C′处,A′C′与⊙O切于点E,连OE并延长交B′C′于F.
设⊙O与直线l切于点D,连OD,则OE⊥A′C′,OD⊥直线l,
由切线长定理可知C′E=C′D,设C′D=x,则C′E=x,易知C′F=
x,
∴
x+x=1,
解得:x=
-1,
∴CC′=5-1-(
-1)=5-
,
∴点C运动的时间为(5-
)÷(2+0.5)=2-
,
则点B运动的距离为2×(2-
)=4-
;
(2)∵△ABC与⊙O从开始运动到最后一次相切时,是AB与圆相切,且圆在AB的左侧,
故路程差为6,速度差为1,
∴从开始运动到最后一次相切的时间为6秒;
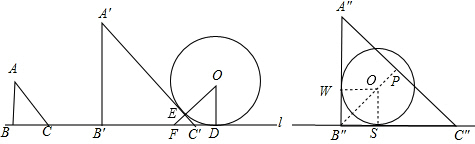
(3)不存在,理由为:△ABC与⊙O的公共部分等于⊙O的面积,即使△ABC的三边与⊙O相切,
∵△ABC与⊙O从开始运动到第二次相切时,路程差为4,速度差为1,
∴从开始运动到第二次相切的时间为4秒,此时△ABC移至△A″B″C″处,A″B″=1+4×
=3,
连接B″O并延长交A″C″于点P,易证B″P⊥A″C″,且OP=
-
=
<1,
∴此时⊙O与A″C″相交,
∴不存在.
设⊙O与直线l切于点D,连OD,则OE⊥A′C′,OD⊥直线l,
由切线长定理可知C′E=C′D,设C′D=x,则C′E=x,易知C′F=
| 2 |
∴
| 2 |
解得:x=
| 2 |
∴CC′=5-1-(
| 2 |
| 2 |
∴点C运动的时间为(5-
| 2 |
2
| ||
| 5 |
则点B运动的距离为2×(2-
2
| ||
| 5 |
4
| ||
| 5 |
(2)∵△ABC与⊙O从开始运动到最后一次相切时,是AB与圆相切,且圆在AB的左侧,
故路程差为6,速度差为1,
∴从开始运动到最后一次相切的时间为6秒;
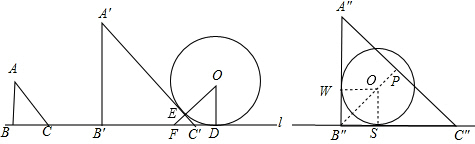
(3)不存在,理由为:△ABC与⊙O的公共部分等于⊙O的面积,即使△ABC的三边与⊙O相切,
∵△ABC与⊙O从开始运动到第二次相切时,路程差为4,速度差为1,
∴从开始运动到第二次相切的时间为4秒,此时△ABC移至△A″B″C″处,A″B″=1+4×
| 1 |
| 2 |
连接B″O并延长交A″C″于点P,易证B″P⊥A″C″,且OP=
3
| ||
| 2 |
| 2 |
| ||
| 2 |
∴此时⊙O与A″C″相交,
∴不存在.
点评:此题考查了圆的综合题,涉及的知识有:圆与直线的位置关系,切线长定理,切线的性质,平移的性质,以及等腰直角三角形的性质,利用了数形结合的思想,是一道较为复杂的试题.

练习册系列答案
相关题目
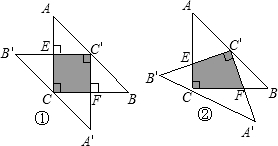 A′B′上?试说明理由.
A′B′上?试说明理由.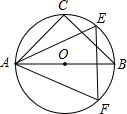 如图,等腰直角△ABC和等边△AEF都是半径为R的圆的内接三角形.
如图,等腰直角△ABC和等边△AEF都是半径为R的圆的内接三角形.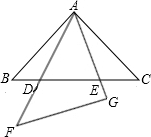 点E不与点C重合),设BE=m,CD=n.
点E不与点C重合),设BE=m,CD=n.