题目内容
19.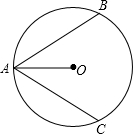 已知:如图,AB,AC是⊙O的两条弦,AO平分∠BAC.求证:$\widehat{AB}$=$\widehat{AC}$.
已知:如图,AB,AC是⊙O的两条弦,AO平分∠BAC.求证:$\widehat{AB}$=$\widehat{AC}$.
分析 由OA平分∠BAC 可推得OD=OE,进而推出AB=CD,根据弦与弧之间的关系即可证得结论.
解答  证明:过点O作OD⊥AB于D,OE⊥AC于E,过点O作OD⊥AB于D,OE⊥AC于E,
证明:过点O作OD⊥AB于D,OE⊥AC于E,过点O作OD⊥AB于D,OE⊥AC于E,
∵OA平分∠BAC,
∴OD=OE,
∴AB=CD,
∴$\widehat{AB}=\widehat{AC}$.
点评 本题主要考了弧和弦的关系,角平分线的性质,关键在于正确的做出辅助线.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
10.抛物线y=x2-2x+1的对称轴是( )
| A. | 直线x=1 | B. | 直线x=-1 | C. | 直线x=2 | D. | 直线x=-2 |
14. 如图,在矩形ABCD中,AB=4,AD=3,若以点A为圆心,以4为半径作⊙A,则下列各点在⊙A外的是( )
如图,在矩形ABCD中,AB=4,AD=3,若以点A为圆心,以4为半径作⊙A,则下列各点在⊙A外的是( )
 如图,在矩形ABCD中,AB=4,AD=3,若以点A为圆心,以4为半径作⊙A,则下列各点在⊙A外的是( )
如图,在矩形ABCD中,AB=4,AD=3,若以点A为圆心,以4为半径作⊙A,则下列各点在⊙A外的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
9.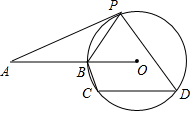 如图,AP为☉O的切线,P为切点,若∠A=20°,C、D为圆周上两点,且∠PDC=60°,则∠OBC等于( )
如图,AP为☉O的切线,P为切点,若∠A=20°,C、D为圆周上两点,且∠PDC=60°,则∠OBC等于( )
 如图,AP为☉O的切线,P为切点,若∠A=20°,C、D为圆周上两点,且∠PDC=60°,则∠OBC等于( )
如图,AP为☉O的切线,P为切点,若∠A=20°,C、D为圆周上两点,且∠PDC=60°,则∠OBC等于( )| A. | 55° | B. | 65° | C. | 70° | D. | 75° |
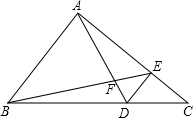 已知△ABC,其中DE与AB平行,已知△DEC的面积为5,且S△ABF:S△AEF=4:1,求△ABC的面积是80.
已知△ABC,其中DE与AB平行,已知△DEC的面积为5,且S△ABF:S△AEF=4:1,求△ABC的面积是80.