题目内容
已知:OA⊥OC于O,OB⊥OD于O,∠BOC=24°;
(1)求:∠AOD的度数;
(2)若∠BOC=α(0°<α<90°),其他条件不变.求:∠AOD的度数;
(3)根据(1)(2)的计算结果,在(2)的条件下,推断∠BOC与∠AOD的关系,并证明。
(1)求:∠AOD的度数;
(2)若∠BOC=α(0°<α<90°),其他条件不变.求:∠AOD的度数;
(3)根据(1)(2)的计算结果,在(2)的条件下,推断∠BOC与∠AOD的关系,并证明。

解:(1)∵OA⊥OC,∠BOC=24°,
∴∠AOB=∠AOC-∠BOC=90°-24°=66°,
∵OB⊥OD于O,
∴∠BOD=90°,
∴∠AOD=∠BOD+∠AOB=90°+66°=156°;
(2)∵OA⊥OC,∠BOC=α°,
∴∠AOB=∠AOC-∠BOC=90°-α°,
∵OB⊥OD于O,
∴∠BOD=90°,
∴∠AOD=∠BOD+∠AOB=90°+90°-α°=(180-α)°;
(3)根据(1)(2)的计算结果,可知,∠AOD=(180-α)°,∠BOC=α°,
∴∠BOC与∠AOD的关系是互补。
∴∠AOB=∠AOC-∠BOC=90°-24°=66°,
∵OB⊥OD于O,
∴∠BOD=90°,
∴∠AOD=∠BOD+∠AOB=90°+66°=156°;
(2)∵OA⊥OC,∠BOC=α°,
∴∠AOB=∠AOC-∠BOC=90°-α°,
∵OB⊥OD于O,
∴∠BOD=90°,
∴∠AOD=∠BOD+∠AOB=90°+90°-α°=(180-α)°;
(3)根据(1)(2)的计算结果,可知,∠AOD=(180-α)°,∠BOC=α°,
∴∠BOC与∠AOD的关系是互补。

练习册系列答案
相关题目
 20、如图所示,已知OA⊥OC于点O,∠AOB=∠COD,试判断OB和OD的位置关系.并说明理由.
20、如图所示,已知OA⊥OC于点O,∠AOB=∠COD,试判断OB和OD的位置关系.并说明理由. 反比例函数
反比例函数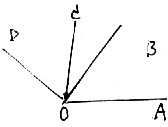 已知:OA⊥OC于O,OB⊥OD于O,∠BOC=24°.
已知:OA⊥OC于O,OB⊥OD于O,∠BOC=24°.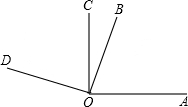 已知:OA⊥OC于O,OB⊥OD于O,∠BOC=24°.
已知:OA⊥OC于O,OB⊥OD于O,∠BOC=24°.