题目内容
 反比例函数y=
反比例函数y=| k |
| x |
| k |
| x |
| k |
| x |
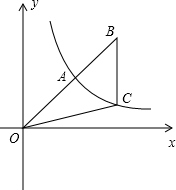
分析:延长BC交x轴于D点,当OA最短时,直线OA为第一象限的角平分线,△OBD为等腰直角三角形,设B(2a,2b),则A(a,b),ab=k,C(2a,
),BC=2b-
,S△BCO=
BC×OD=6,解方程求k.
| k |
| 2a |
| k |
| 2a |
| 1 |
| 2 |
解答: 解:延长BC交x轴于D点,
解:延长BC交x轴于D点,
依题意,可知OA最短时,直线OA为第一象限的角平分线,即△OBD为等腰直角三角形,
设B(2a,2b),则A(a,b),ab=k,C(2a,
),BC=2b-
,
∴S△BCO=
BC×OD=
(2b-
)×2a=6,
即4ab-k=12,4k-k=12,
解得k=4.
故答案为:4.
 解:延长BC交x轴于D点,
解:延长BC交x轴于D点,依题意,可知OA最短时,直线OA为第一象限的角平分线,即△OBD为等腰直角三角形,
设B(2a,2b),则A(a,b),ab=k,C(2a,
| k |
| 2a |
| k |
| 2a |
∴S△BCO=
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2a |
即4ab-k=12,4k-k=12,
解得k=4.
故答案为:4.
点评:本题考查了反比例函数的综合运用.关键是根据点的位置设点的坐标,根据反比例函数的性质及三角形面积公式列方程求解.

练习册系列答案
相关题目
 如图,l2是反比例函数y=
如图,l2是反比例函数y= 反比例函数y=
反比例函数y= 若一次函数y=ax+b与反比例函数
若一次函数y=ax+b与反比例函数 (2012•东莞)如图,直线y=2x-6与反比例函数y=
(2012•东莞)如图,直线y=2x-6与反比例函数y=