题目内容
 如图,在Rt△ABC中,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE=3.8cm,则BC=
如图,在Rt△ABC中,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE=3.8cm,则BC=考点:角平分线的性质,含30度角的直角三角形
专题:
分析:根据角平分线上的点到角的两边距离相等可得CD=DE,再求出∠CAD=∠BAD=∠B=30°,再根据直角三角形30°所对的直角边等于斜边的一半可得AD=2CD,根据等角对等边可得BD=AD,然后利用BC=CD+BD计算即可得解.
解答:解:∵AD平分∠CAB,∠C=90°,
∴CD=DE=3.8cm,
∵∠CAB=60°,AD平分∠CAB,
∴∠CAD=∠BAD=∠B=30°,
∴AD=2CD=2×3.8=7.6cm,
BD=AD=7.6cm,
∴BC=CD+BD=3.8+7.6=11.4cm.
故答案为:11.4.
∴CD=DE=3.8cm,
∵∠CAB=60°,AD平分∠CAB,
∴∠CAD=∠BAD=∠B=30°,
∴AD=2CD=2×3.8=7.6cm,
BD=AD=7.6cm,
∴BC=CD+BD=3.8+7.6=11.4cm.
故答案为:11.4.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,直角三角形30°所对的直角边等于斜边的一半的性质,等角对等边的性质,熟记各性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在Rt△ABC中,∠ABC是直角,AB=3,BC=4,P是BC边上的动点.设BP=x,若能在AC边上找到一点Q,使∠BQP=90°,则x的取值范围是( )
如图,在Rt△ABC中,∠ABC是直角,AB=3,BC=4,P是BC边上的动点.设BP=x,若能在AC边上找到一点Q,使∠BQP=90°,则x的取值范围是( )| A、2.4≤x≤4 |
| B、3≤x≤4 |
| C、2.5≤x≤4 |
| D、3<x≤4 |
肥皂泡的泡壁厚度大约是0.0007mm,0.0007用科学计数法表示为( )
| A、0.7×10-3 |
| B、7×10-3 |
| C、7×10-4 |
| D、7×10-5 |
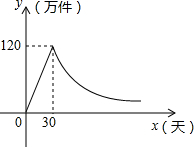 某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图),现己知上市30天时,当日销售量为120万件.
某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图),现己知上市30天时,当日销售量为120万件.