题目内容
6.你是“航天迷”吗?人们研究发现,当火箭竖直向上发射时,它的高度h(m)与时间t(s)的关系可以用公式h=-5t2+v0t+h0表示.其中h0(m)是发射时的高度,v0(m/s)是发射时的速度.如果v0=150(m/s),h0=10(m).你能用学过的知识计算经过多长时间,火箭到达它的最高点吗?(假设没有第二次点燃燃料),最高点的高度是多少?经过多长时间,火箭到达的高度为1000m?(精确到0.01s)分析 要求经过多长时间,火箭达到它的最高点,即求二次函数的最值问题,可以用公式法或配方法求出,把y=1000代入函数表达式解方程即可求出经过多长时间,火箭到达的高度为1000m.
解答 解:h=-5t2+150t+10
=(-5t2+150t)+10
=-5(t2-30t)+10
=-5(t2-30t+225-225)+10
=-5(t-15)2+1135
当t=15s时,h有最大值,h=1135m,
令y=1000,则1000=-5(t-15)2+1135,
解得:t1=15+3$\sqrt{3}$,t2=15-3$\sqrt{3}$
∴经过(15-3$\sqrt{3}$)s,火箭到达的高度为1000m.
点评 此题主要考查了二次函数的实际应用以及二次函数与一元二次方程的关系,正确理解题意是解决问题的关键.

练习册系列答案
相关题目
1.已知二次函数y=ax2,下列说法不正确的是( )
| A. | 对称轴为y轴 | B. | 当a<0,x≠0时,y轴总为负值 | ||
| C. | 当a>0时,y有最小值0 | D. | 当a<0,x<0时,y随x的增大而减小 |
11.某洗衣粉厂上月生产了30000袋洗衣粉.每袋标准重量450克,质量检测部分从中抽出了20袋进行检测,超过或不足标准重量的分别用“+”和“-”表示,记录如下:
(1)通过计算估计本厂上月生产的洗衣粉平均每袋多少克?
(2)厂家规定超过或不足的部分大于5克时,不能出厂销售.若每袋洗衣粉的定价为2.30元,估计本厂上月生产的洗衣粉销售的总金额为多少元?
| 超过或不足(克) | -6 | -3 | -2 | 0 | +1 | +4 | +5 |
| 袋数 | 1 | 1 | 1 | 6 | 5 | 2 | 4 |
(2)厂家规定超过或不足的部分大于5克时,不能出厂销售.若每袋洗衣粉的定价为2.30元,估计本厂上月生产的洗衣粉销售的总金额为多少元?
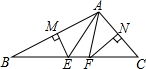 已知:如图,在△ABC中,AB的垂直平分线分别交AB、BC于点M、E,AC的垂直平分线分别交AC、BC于点N、F,∠B=27°,∠BAC=2∠C.求∠EAF的度数.
已知:如图,在△ABC中,AB的垂直平分线分别交AB、BC于点M、E,AC的垂直平分线分别交AC、BC于点N、F,∠B=27°,∠BAC=2∠C.求∠EAF的度数. “水幕电影”的工作原理是把影像打在抛物线状的水幕上,通过光学原理折射出图象,水幕是由若干个水嘴喷出的水柱组成的(如图),水柱的最高点为P,AB=2m,BP=10m,水嘴高AD=6m,以A为坐标原点,AB所在的直线为x轴,AD所在的直线为y轴建立平面直角坐标系,求图中抛物线的解析式.
“水幕电影”的工作原理是把影像打在抛物线状的水幕上,通过光学原理折射出图象,水幕是由若干个水嘴喷出的水柱组成的(如图),水柱的最高点为P,AB=2m,BP=10m,水嘴高AD=6m,以A为坐标原点,AB所在的直线为x轴,AD所在的直线为y轴建立平面直角坐标系,求图中抛物线的解析式.