题目内容
 如图,一次函数y=x+2交x轴于A点,交y轴于B点,直线AB绕A点旋转,交y轴于B′点;在旋转的过程中,当△AOB′的面积恰好等于△AOB面积的一半;求此时直线AB′的解析式________.
如图,一次函数y=x+2交x轴于A点,交y轴于B点,直线AB绕A点旋转,交y轴于B′点;在旋转的过程中,当△AOB′的面积恰好等于△AOB面积的一半;求此时直线AB′的解析式________.
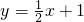 或
或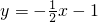
分析:此题,分两种情况:直线AB绕点A顺时针旋转和逆时针旋转.根据三角形的面积公式知OB′=
 OB,所以利用待定系数法来求求旋转后的直线方程即可.
OB,所以利用待定系数法来求求旋转后的直线方程即可.解答:∵一次函数y=x+2交x轴于A点,交y轴于B点,
∴A(-2,2),B(0,2).
∵△AOB′的面积恰好等于△AOB面积的一半,
∴
 OA•OB=
OA•OB= OA•OB′,则OB′=
OA•OB′,则OB′= OB,
OB,∴B′(0,1)或B′(0,-1).
设直线AB′的解析式为y=kx+b(k≠0).
当B′的坐标是(0,1)时,
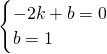 ,
,解得,
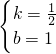 ,
,∴直线AB′的解析式为:y=
 x+1.
x+1.同理,当B′的坐标是(0,-1)时,直线AB′的解析式为:y=-
 x-1.
x-1.综上所述,直线AB′的解析式为:
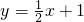 或
或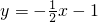 .
.故答案是:
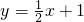 或
或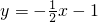 .
.点评:本题考查了一次函数图象与几何变换.解题时,要分类讨论,以防漏掉另一个答案.

练习册系列答案
相关题目
 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y= 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数