题目内容
已知实数x、y满足 x2+2x+y-1=0,则x+2y的最大值为 .
x2+2x+y-1=0,则x+2y的最大值为 .
 .
.
【解析】
试题分析:因为 x+2x+y-1=0,所以y=-
x+2x+y-1=0,所以y=- x-2x+1,所以x+2y=x-x-4x+2=-x-3x+2=-(x+
x-2x+1,所以x+2y=x-x-4x+2=-x-3x+2=-(x+ )+
)+ ,当x=-
,当x=- 时,x+2y有最大值,(x+2y)的最大值=
时,x+2y有最大值,(x+2y)的最大值= .
.
故答案为: .
.
考点:二次函数的最大值.
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 和7的两个点的距离相等的点所表示的数为______________.
和7的两个点的距离相等的点所表示的数为______________.




 B.
B. C.
C. D.
D.
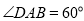 ,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.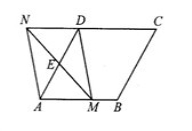
 B.10 C.4 D.2
B.10 C.4 D.2


