题目内容
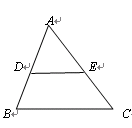
利用“等积”计算或说理是一种很巧妙的方法, 就是一个面积从两个不同的角度表示。如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=3,AC=4,求CD的长。
解题思路:利用勾股定理易得AB=5利用
 ,可得到CD=2.4
,可得到CD=2.4
请你利用上述方法解答下面问题:
(1) 如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=5,AC=12,求CD的长。

(2)如图乙,△ABC是边长为2的等边三角形,点D是BC边上的
任意一点,DE⊥AB于E点,DF⊥AC于F点,求DE+DF的值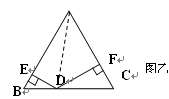
解题思路:利用勾股定理易得AB=5利用
 ,可得到CD=2.4
,可得到CD=2.4请你利用上述方法解答下面问题:
(1) 如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=5,AC=12,求CD的长。

(2)如图乙,△ABC是边长为2的等边三角形,点D是BC边上的
任意一点,DE⊥AB于E点,DF⊥AC于F点,求DE+DF的值

(1) ,可得到CD=
,可得到CD= ……3′
……3′
(2)等边三角形ABC的高线长是 ……5′
……5′
由 得
得 BC×
BC× =
= AB×DE+
AB×DE+ AC×DF
AC×DF
∵BC=" AB=" AC ∴DE+DF= ……8′
……8′
 ,可得到CD=
,可得到CD= ……3′
……3′(2)等边三角形ABC的高线长是
 ……5′
……5′由
 得
得 BC×
BC× =
= AB×DE+
AB×DE+ AC×DF
AC×DF∵BC=" AB=" AC ∴DE+DF=
 ……8′
……8′(1)先由勾股定理求出AB,再由题干的解题思路得 BC×AC=
BC×AC= AB×CD,代入数据即可得出CD;
AB×CD,代入数据即可得出CD;
(2)根据分析,过点A作AE⊥BC,垂足为E,再根据勾股定理得出AE,由S△ABC=S△ADB+S△ADC求出DE+DF即可.
 BC×AC=
BC×AC= AB×CD,代入数据即可得出CD;
AB×CD,代入数据即可得出CD;(2)根据分析,过点A作AE⊥BC,垂足为E,再根据勾股定理得出AE,由S△ABC=S△ADB+S△ADC求出DE+DF即可.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目

 ,则它的顶角为 ( ★ )
,则它的顶角为 ( ★ )
 或
或