题目内容

12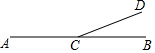．如图，直线AB与射线CD相交于点C，若∠BCD=20°，则∠ACD=（　　）
A．70°B．120°C．150°D．160°

分析 根据平角的定义，可得∠ACD=180°-∠BCD，由此计算即可．

解答 解：∵∠ACD+∠BCD=180°，∠BCD=20°，
∴∠ACD=180°-20°=160°，
故选D．

点评 本题考查平角的定义，邻补角的性质等知识，解题的关键是熟练掌握邻补角的性质，属于中考基础题．

练习册系列答案
相关题目
3．已知|x|=3，y=2，且x＞y，则x+y的值为（　　）
A．-5B．-1C．5或-1D．5
4．在实数$\sqrt{5}$、$\frac{1}{3}$、0、3.1415、π、$\root{3}{3}$、$\sqrt{4}$、0.1010010001中，无理数的个数是（　　）
A．1B．2C．3D．4
1．在今年“全国助残日”捐款活动中，某班级第一小组7名同学积极捐出自己的零花钱，奉献自己的爱心．他们捐款的数额分别是（单位：元）50，20，50，30，25，50，55，这组数据的众数和中位数分别是50，50．
7．如图，∠ACB=90°，CD⊥AB于D，下列结论错误的是（　　）
A．∠1=∠BB．∠2=∠1
C．∠2和∠A都是∠B的余角D．AC•BC=AB•CD
17．在一个m（m≥3，m为整数）位的正整数中，若从左到右第n（n≤m，n为正整数）位上的数字与从右到左第n位上的数字之和都等于同一个常数k（k为正整数），则称这样的数为“对称等和数”．例如在正整数3186中，因为3+6=1+8=9，所以3186是“对称等和数”，其中k=9．再如在正整数53697中，因为5+7=3+9=6+6=12，所以53697是“对称等和数”，其中k=12．
（1）已知在一个能被11整除的四位“对称等和数”中k=4．设这个四位“对称等和数”的千位上的数字为s（1≤s≤9，s为整数），百位上的数字为t（0≤t≤9，t为整数），$\frac{st}{2}$是整数，求这个四位“对称等和数”；
（2）已知数A，数B，数C都是三位“对称等和数”．A=$\overline{1a5}$（1≤a≤9，a为整数），设数B十位上的数字为x（0≤x≤9，x为整数），数C十位上的数字为y（0≤y≤9，y为整数），若A+B+C=1800，求证：y=-x+15．
4．下列推理中，以“等量代换”为推理数据的是（　　）
A．∵∠1=∠2，∠2=∠3，∴∠1=∠3B．∵a∥b，b∥c，∴a∥c
C．∵∠1=∠2，∴$\frac{1}{2}$∠1=$\frac{1}{2}$∠2D．∵∠1+∠2=90°，∠1+∠3=90°，∴∠2=∠3
1．计算：（π-2017）0+$\sqrt{12}$+|$\sqrt{3}$-2|+（$\frac{1}{2}$）-1．
2．等腰△ABC中，AB=AC=6cm，∠A=150°，则△ABC的面积为（　　）
A．9cm2B．18cm2C．6cm2D．36cm2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网