题目内容
如图,在平面直角坐标系 中,矩形
中,矩形 的边
的边 在
在 轴上,且
轴上,且 ,
, ,直线
,直线 经过点
经过点 ,交
,交 轴于点
轴于点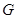 .
.
(1)点 、
、 的坐标分别是
的坐标分别是 ( ),
( ), ( );
( );
(2)求顶点在直线 上且经过点
上且经过点 的抛物线的解析式;
的抛物线的解析式;
(3)将(2)中的抛物线沿直线 向上平移,平移后的抛物线交
向上平移,平移后的抛物线交 轴于点
轴于点 ,顶点为点
,顶点为点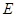 .求出当
.求出当 时抛物线的解析式.
时抛物线的解析式.
(1) C(4,2 ),D(1,2
),D(1,2 );(2)
);(2) ;(3)y=
;(3)y= (x﹣
(x﹣ )2﹣
)2﹣ .
.
解析试题分析:(1)根据题意可得点C的纵坐标为3,代入直线解析式可得出点C的横坐标,继而也可得出点D的坐标;
(2)由题意可得点C和点D关于抛物线的对称轴对称,从而得出抛物线的对称轴为x= ,再由抛物线的顶点在直线y=
,再由抛物线的顶点在直线y= x?2
x?2 上,可得出顶点坐标为(
上,可得出顶点坐标为( ,
, ),设出顶点式,代入点C的坐标即可得出答案.
),设出顶点式,代入点C的坐标即可得出答案.
试题解析:(1)C(4,2 ),D(1,2
),D(1,2 )
)
(2)由二次函数对称性得,顶点横坐标为 ,
,
令x= ,则
,则 ,
,
∴顶点坐标为( ,
, ),
),
∴设抛物线解析式为 ,把点D(1,
,把点D(1, )代入得,
)代入得,
∴解析式为
(3)设顶点E在直线上运动的横坐标为m,则E(m, )
)
∴可设解析式为 ,
,
当GE=EF时,FG= m,则F(0,
m,则F(0, m﹣
m﹣ ),
),
代入解析式得: m2+
m2+ m﹣
m﹣ =
= m﹣
m﹣ ,
,
解得m=0(舍去),m= ,
,
此时所求的解析式为:y= (x﹣
(x﹣ )2﹣
)2﹣
考点:二次函数综合题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 EF,请求出点P的坐标;
EF,请求出点P的坐标;
 ,且空调采购单价不低于1200元,问该商家共有几种进货方案?
,且空调采购单价不低于1200元,问该商家共有几种进货方案? ,点P从O点出发,沿边OA、AB、BC匀速运动,点Q从点C出发,以1cm/s的速度沿边CO匀速运动。点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点P运动的时间为t(s),△CPQ的面积为S(cm2), 已知S与t之间的函数关系如图2中曲线段OE、线段EF与曲线段FG给出.
,点P从O点出发,沿边OA、AB、BC匀速运动,点Q从点C出发,以1cm/s的速度沿边CO匀速运动。点P与点Q同时出发,其中一点到达终点,另一点也随之停止运动.设点P运动的时间为t(s),△CPQ的面积为S(cm2), 已知S与t之间的函数关系如图2中曲线段OE、线段EF与曲线段FG给出.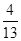 ?
?
 与
与 轴交于点A,B,与y轴交于点C,其中点B的坐标为
轴交于点A,B,与y轴交于点C,其中点B的坐标为 .
. (B的对应点为
(B的对应点为 ,C的对应点为
,C的对应点为 ),使其经过(2)中所得抛物线G的顶点M,且与抛物线G另有一个交点N,求点
),使其经过(2)中所得抛物线G的顶点M,且与抛物线G另有一个交点N,求点 的距离
的距离 的取值范围.
的取值范围.
 的图象经过(
的图象经过( ,0)和(
,0)和( ,0)两点.
,0)两点. <x<1时,y的取值范围.
<x<1时,y的取值范围.
 (b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,–1),C的坐标为(4,3),直角顶点B在第四象限.
(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,–1),C的坐标为(4,3),直角顶点B在第四象限. 取最大值时,点Q的坐标为________.
取最大值时,点Q的坐标为________.

 中,抛物线
中,抛物线 与x轴交于点A(-2,0)和点B,与y轴交于点C(0,
与x轴交于点A(-2,0)和点B,与y轴交于点C(0, ),线段AC上有一动点P从点A出发,以每秒1个单位长度的速度向点C移动,线段AB上有另一个动点Q从点B出发,以每秒2个单位长度的速度向点A移动,两动点同时出发,设运动时间为t秒.
),线段AC上有一动点P从点A出发,以每秒1个单位长度的速度向点C移动,线段AB上有另一个动点Q从点B出发,以每秒2个单位长度的速度向点A移动,两动点同时出发,设运动时间为t秒.