Question

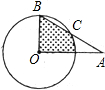如图，⊙O的半径为2cm，∠AOB=90°，∠A=30°，AB交⊙O于C，则图中阴影部分的面积为________cm²．

Answer 1

π+
分析：连接OC，则△OBC是等边三角形，根据阴影部分的面积是=扇形BOD的面积-（扇形BOC的面积-S_△OBC），分别求出两个扇形的面积和等边三角形的面积即可求解．
解答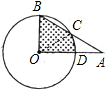：解：连接OC，
则扇形BOD的面积是：=π，
∵∠AOB=90°，∠A=30°，
∴∠B=90°-30°=60°，
又∵OB=OC
∴△OBC是等边三角形，
∴扇形BOC的面积是：=π，S_△OBC==，
∴阴影部分的面积是=扇形BOD的面积-（扇形BOC的面积-S_△OBC）=π-（π-）=π+．
故答案是：π+．
点评：本题考查了扇形的面积公式以及等边三角形的面积，不规则的图形可以通过规则图形的面积的和或差来计算，理解阴影部分的面积是=扇形BOD的面积-（扇形BOC的面积-S_△OBC）是关键．