Question

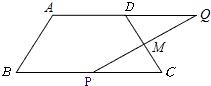8、如图，在梯形ABCD中，AD∥BC，AD=5cm，BC=8cm，M是CD的中点，P是BC边上的一动点（P与B，C不重合），连接PM并延长交AD的延长线于Q．
（1）试说明△PCM≌△QDM．
（2）当P在B、C之间运动到什么位置时，四边形ABPQ是平行四边形？并说明理由．

Answer 1

分析：（1）要证明△PCM≌△QDM，可以根据两个三角形全等四个定理，即AAS、ASA、SAS、SSS中的ASA．求证∠QDM=∠PCM，DM=CM，∠DMQ=∠CMP．
（2）得出P在B、C之间运动的位置，根据一组对边平行且相等的四边形是平行四边形得出．

解答：解：（1）∵AD∥BC
∴∠QDM=∠PCM
∵M是CD的中点，
∴DM=CM，
∵∠DMQ=∠CMP
∴△PCM≌△QDM．
（2）当四边形ABPQ是平行四边形时，PB=AQ，BC-CP=AD+QD，CP=（8-5）÷2=1.5．

点评：本题综合考查全等三角形、平行四边形的判定，熟练掌握平行四边形的性质和判定方法是解题的关键．