题目内容
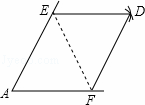
如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
(1)请你判断所画四边形的性状,并说明理由;
(2)连接EF,若AE=8厘米,∠A=60°,求线段EF的长.

考点:
菱形的判定与性质;等边三角形的判定与性质.
分析:
(1)由AE=AF=ED=DF,根据四条边都相等的四边形是菱形,即可证得:四边形AEDF是菱形;
(2)首先连接EF,由AE=AF,∠A=60°,可证得△EAF是等边三角形,则可求得线段EF的长.
解答:
解:(1)菱形.
理由:∵根据题意得:AE=AF=ED=DF,
∴四边形AEDF是菱形;
(2)连接EF,
∵AE=AF,∠A=60°,
∴△EAF是等边三角形,
∴EF=AE=8厘米.
点评:
此题考查了菱形的判定与性质以及等边三角形的判定与性质.此题比较简单,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 17、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长:△ABC的周长=
17、如图,点D、E分别是△ABC边AB、AC上的点,且DE∥BC,BD=2AD,那么△ADE的周长:△ABC的周长=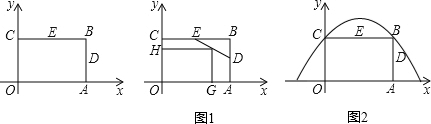
 (2013•武汉模拟)如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( )
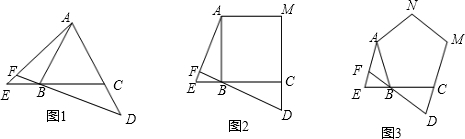
(2013•武汉模拟)如图,点I和O分别是△ABC的内心和外心,则∠AIB和∠AOB的关系为( ) 如图,点E、D分别是正三角形ABC中以C点为顶点的一边延长线和另一边反向延长线上的点,且BE=CD,DB延长线交于AE于点F,则∠AFB的度数是
如图,点E、D分别是正三角形ABC中以C点为顶点的一边延长线和另一边反向延长线上的点,且BE=CD,DB延长线交于AE于点F,则∠AFB的度数是