题目内容
关于x的方程（a-6）x2-8x+6=0有实数根，则整数a的最大值是
- A.6
- B.7
- C.8
- D.9
C
分析：方程有实数根，应分方程是一元二次方程与不是一元二次方程，两种情况进行讨论，当不是一元二次方程时，a-6=0，即a=6；
当是一元二次方程时，有实数根，则△≥0，求出a的取值范围，取最大整数即可．
解答：当a-6=0，即a=6时，方程是-8x+6=0，解得x=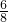
=
；
当a-6≠0，即a≠6时，△=（-8）2-4（a-6）×6=208-24a≥0，解上式，得a≤
≈8.6，
取最大整数，即a=8．故选C．
点评：通过△求出a的取值范围后，再取最大整数．
分析：方程有实数根，应分方程是一元二次方程与不是一元二次方程，两种情况进行讨论，当不是一元二次方程时，a-6=0，即a=6；
当是一元二次方程时，有实数根，则△≥0，求出a的取值范围，取最大整数即可．
解答：当a-6=0，即a=6时，方程是-8x+6=0，解得x=
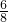=；当a-6≠0，即a≠6时，△=（-8）2-4（a-6）×6=208-24a≥0，解上式，得a≤
≈8.6，取最大整数，即a=8．故选C．
点评：通过△求出a的取值范围后，再取最大整数．
练习册系列答案
考前必练系列答案
相关题目