题目内容
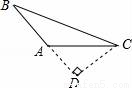
3. 如图,已知A(2,0),B(4,0),点P是直线y=x上一点,当PA+PB最小时,点P的坐标为($\frac{4}{3}$,$\frac{4}{3}$).
如图,已知A(2,0),B(4,0),点P是直线y=x上一点,当PA+PB最小时,点P的坐标为($\frac{4}{3}$,$\frac{4}{3}$).
分析 先作出点A关于直线y=x的对称点A′,再连接A′B,求出直线A′B的函数解析式,再联立直线y=x列方程组即可求解.
解答  解:如图,作A关于直线y=x的对称点A′,
解:如图,作A关于直线y=x的对称点A′,
则PA=PA′,
故PA+PB=PA′+PB,
由图知,只有当A、P、B共线时,PA+PB最小,
又由A与A′关于y=x对称知,A′(0,2),
由A′、B两点坐标得直线A′B的解析式为y=-$\frac{1}{2}$x+2,
联立 $\left\{\begin{array}{l}{y=x}\\{y=-\frac{1}{2}x+2}\end{array}\right.$,
解得 x=y=$\frac{4}{3}$,
故当PA+PB最小时,P的坐标为:($\frac{4}{3}$,$\frac{4}{3}$).
故答案为:($\frac{4}{3}$,$\frac{4}{3}$).
点评 此题主要考查了轴对称--最短路线问题,综合运用了一次函数和方程组的知识,综合性较强,做题的关键是正确作出图形.

练习册系列答案
相关题目
14.若关于x、y的多项式3nx2-x2+5x+8-(-7x2-3y+5x)的值与x无关,则n=( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
8.南京长江四桥线路全长约29000米,将29000用科学记数法表示为( )
| A. | 0.29×105 | B. | 2.9×103 | C. | 2.9×104 | D. | 29×103 |
15.一件夹克衫先按成本提高50%标价,再以8折(标价的80%)出售,结果获利20元,若设这件夹克衫的成本是x元,根据题意,可得到的方程是( )
| A. | (1+50%)x×80%=x-20 | B. | (1+50%)x×80%=x+20 | C. | (1+50%x)×80%=x-20 | D. | (1+50%x)×80%=x+20 |
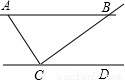
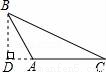
 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=3,则BC的长为3+$\sqrt{5}$.
如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=3,则BC的长为3+$\sqrt{5}$.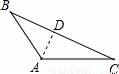 B.
B. 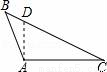
 D.
D.