Question

如图，已知AE平行于BC且平分∠DAC．
求证：AB=AC．

Answer 1

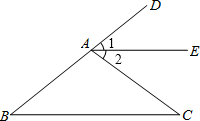证明：如图，∵AE∥BC，
∴∠1=∠B，∠2=∠C，
∵AE平分∠DAC，
∴∠1=∠2，
∴∠B=∠C，
∴AB=AC．
分析：根据两直线平行，同位角相等可得∠1=∠B，两直线平行，内错角相等可得∠2=∠C，再根据角平分线的定义可得∠1=∠2，然后求出∠B=∠C，再根据等角对等边的性质即可得证．
点评：本题考查了等腰三角形的判定与性质，平行线的性质，是基础题，比较简单，熟记性质是解题的关键，用弧线加数字表示角更形象直观．