题目内容
阅读理解并回答问题.
(1)观察下列各式:
=
=
-
,
=
=
-
,
=
=
-
,
=
=
-
,…
(2)请你猜想出表示(1)中的特点的一般规律,用含x(x表示整数)的等式表示
=
-
-
(3)请利用上述规律,解方程
+
+
+
+
=
.
(1)观察下列各式:
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 12 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 20 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
(2)请你猜想出表示(1)中的特点的一般规律,用含x(x表示整数)的等式表示
| 1 |
| x(x+1) |
| 1 |
| x |
| 1 |
| x+1 |
| 1 |
| x |
| 1 |
| x+1 |
(3)请利用上述规律,解方程
| 1 |
| (x-4)(x-3) |
| 1 |
| (x-3)(x-2) |
| 1 |
| (x-2)(x-1) |
| 1 |
| (x-1)x |
| 1 |
| x(x+1) |
| 1 |
| x+1 |
分析:(2)观察(1),可得规律:
=
-
;
(3)由(2)中的规律,可将原方程化为
-
+
-
+
-
+
-
+
-
=
,即可得
=
,解此方程即可求得答案.
| 1 |
| x(x+1) |
| 1 |
| x |
| 1 |
| x+1 |
(3)由(2)中的规律,可将原方程化为
| 1 |
| x-4 |
| 1 |
| x-3 |
| 1 |
| x-3 |
| 1 |
| x-2 |
| 1 |
| x-2 |
| 1 |
| x-1 |
| 1 |
| x-1 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x+1 |
| 1 |
| x+1 |
| 1 |
| x-4 |
| 2 |
| x+1 |
解答:解:(2)由(1)可得:
=
-
;
(3)原方程变形为:
-
+
-
+
-
+
-
+
-
=
,
即
=
,
∴x+1=2(x-4),
解得:x=9,
检验:左边=
,右边=
,即x=9是原分式方程的解,
∴原分式方程的解为:x=9.
| 1 |
| x(x+1) |
| 1 |
| x |
| 1 |
| x+1 |
(3)原方程变形为:
| 1 |
| x-4 |
| 1 |
| x-3 |
| 1 |
| x-3 |
| 1 |
| x-2 |
| 1 |
| x-2 |
| 1 |
| x-1 |
| 1 |
| x-1 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x+1 |
| 1 |
| x+1 |
即
| 1 |
| x-4 |
| 2 |
| x+1 |
∴x+1=2(x-4),
解得:x=9,
检验:左边=
| 1 |
| 10 |
| 1 |
| 10 |
∴原分式方程的解为:x=9.
点评:此题考查了分式的加减运算与分式方程的解法.此题难度适中,解题的关键是得到规律:
=
-
.
| 1 |
| x(x+1) |
| 1 |
| x |
| 1 |
| x+1 |

练习册系列答案
相关题目
 =
= =
= -
- =
= =
= ,
, =
= =
= ,
, =
=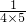 =
= ,
,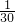 =
=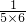 =
=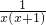 =______.
=______.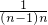 +
+
 +
+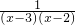 +
+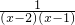 +
+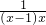 +
+