题目内容
 如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:
如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系: (0≤x≤5),则以下结论不正确的是
(0≤x≤5),则以下结论不正确的是
- A.OB=3
- B.OA=5
- C.AF=2
- D.BF=5
A
分析:设P的坐标是(x,y),过P作PM⊥x轴,于M点,在直角△PFM中,根据勾股定理,即可求得函数的解析式.根据解析式即可判断.
解答: 解:
解:
过P作PM⊥x轴于点M.
设P的坐标是(x,y).直角△PMF中,PM=y,MF=3-x.PM2+MF2=PF2.
∴(3-x)2+y2=(5- x)2.
x)2.
解得:y2=- x2+16.
x2+16.
在上式中,令x=0,解得y=4.过OB=3.故A错误;
在上式中,令y=0,解得:x=5,则AF=OA-OF=5-3=2,故B,C正确;
在直角△OBF中,根据勾股定理即可求得:BF=5,故D正确.
故选A.
点评:本题是函数与三角形相结合的问题,在图形中渗透运动的观点是中考中经常出现的问题.正确求得函数的解析式是解决本题的关键.
分析:设P的坐标是(x,y),过P作PM⊥x轴,于M点,在直角△PFM中,根据勾股定理,即可求得函数的解析式.根据解析式即可判断.
解答:
 解:
解:过P作PM⊥x轴于点M.
设P的坐标是(x,y).直角△PMF中,PM=y,MF=3-x.PM2+MF2=PF2.
∴(3-x)2+y2=(5-
 x)2.
x)2.解得:y2=-
 x2+16.
x2+16.在上式中,令x=0,解得y=4.过OB=3.故A错误;
在上式中,令y=0,解得:x=5,则AF=OA-OF=5-3=2,故B,C正确;
在直角△OBF中,根据勾股定理即可求得:BF=5,故D正确.
故选A.
点评:本题是函数与三角形相结合的问题,在图形中渗透运动的观点是中考中经常出现的问题.正确求得函数的解析式是解决本题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
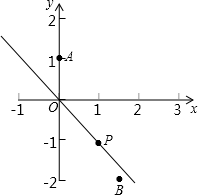 如图,已知点A的坐标为(0,1),点B的坐标为(
如图,已知点A的坐标为(0,1),点B的坐标为(| 3 |
| 2 |
| A、(2,-2) | ||||
| B、(4,-4) | ||||
C、(
| ||||
| D、(5,-5) |
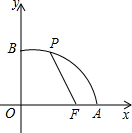 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-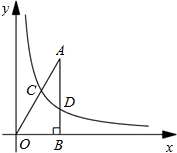 如图,已知点A的坐标为(
如图,已知点A的坐标为(

 如图,已知点A的坐标为(
如图,已知点A的坐标为(