题目内容
11.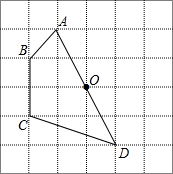 如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转,试解决下列问题:
如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转,试解决下列问题:(1)画出四边形ABCD旋转180°后的图形;
(2)求点C旋转过程中所经过的路径长;
(3)求sin∠BAD的值.
分析 (1)根据中心对称的性质画出点A、B、C、D关于点O中心对称的点A′、B′、C′、D′,从而得到四边形A′B′C′D′;
(2)点C旋转过程中所经过的路径为以点O为圆心,OC为半径,圆心角为180度的弧,然后根据弧长公式计算;
(3)先利用勾股定理计算出AB=$\sqrt{2}$,BD=3$\sqrt{2}$,AD=2$\sqrt{5}$,则根据勾股定理的逆定理可判断△ABD为直角三角形,∠ABD=90°,然后根据正弦的定义求解.
解答 解:(1)如图,四边形A′B′C′D′为所求;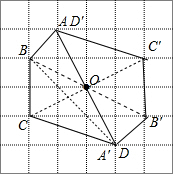
(2)OC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
所以点C旋转过程中所经过的路径长=$\frac{180•π•\sqrt{5}}{180}$=$\sqrt{5}$π;
(3)连结BD,如图,
∵AB=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,BD=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,AD=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴AB2+BD2=AD2,
∴△ABD为直角三角形,∠ABD=90°,
∴sin∠BAD=$\frac{BD}{AD}$=$\frac{3\sqrt{2}}{2\sqrt{5}}$=$\frac{3\sqrt{10}}{10}$
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了勾股定理的逆定理和解直角三角形.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
1.要使代数式$\frac{1}{1+\frac{1}{x+1}}$有意义,则必须( )
| A. | x≠-1或x≠-2 | B. | x≠-1 | C. | x≠-2 | D. | x≠-1且x≠-2 |
2.已知实数a、b满足a2=2-2a,b2=2-2b,则$\frac{b}{{a}^{2}}$+$\frac{a}{{b}^{2}}$=( )
| A. | 5 | B. | 1±$\sqrt{3}$ | C. | 5或1-$\sqrt{3}$ | D. | 5或1±$\sqrt{3}$ |
19.人的大脑每天能记录大约8600万条信息,8600万用科学记数法表示为( )
| A. | 0.86×108 | B. | 8.6×103 | C. | 8.6×107 | D. | 86×102 |
6. 如图所示的物体是一个几何体,其俯视图是( )
如图所示的物体是一个几何体,其俯视图是( )
 如图所示的物体是一个几何体,其俯视图是( )
如图所示的物体是一个几何体,其俯视图是( )| A. |  | B. |  | C. |  | D. |  |
16.已知反比例函数y=-$\frac{k}{x}$图象上三个点的坐标分别是A(-2,y1)、B(-1,y2)、C(2,y3),若y1<y2,则( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y3=y1<y2 |
3.下列计算中正确的是( )
| A. | 3a+2a=a5 | B. | (3ab2)3=9a3b6 | C. | a2•a3=a6 | D. | (-a3)2=a6 |
 阅读材料:
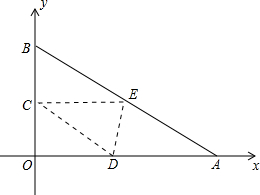
阅读材料: 四边形ABCD是以点O为对称中心的中心对称图形,过点O作OE⊥AC交BC于点E,如果△ABE的周长为24cm,求四边形ABCD的周长.
四边形ABCD是以点O为对称中心的中心对称图形,过点O作OE⊥AC交BC于点E,如果△ABE的周长为24cm,求四边形ABCD的周长.