题目内容
17.三角形的三边长分别为12、16、20,它的三条中位线围成的三角形的周长为24.分析 根据题意画出图形,再根据中位线定理可得DE=$\frac{1}{2}$AC,EF=$\frac{1}{2}$AB,DF=$\frac{1}{2}$CB,进而可得求出△DEF的周长.
解答  解:如图所示:AC=20,AB=16,BC=12,E、D、F分别为BC、AB、AC中点,
解:如图所示:AC=20,AB=16,BC=12,E、D、F分别为BC、AB、AC中点,
∵E、D、F分别为BC、AB、AC中点,
∴DE=$\frac{1}{2}$AC,EF=$\frac{1}{2}$AB,DF=$\frac{1}{2}$CB,
∵AC=20,AB=16,BC=12,
∴DF=6,EF=8,ED=10,
∴△DEF的周长为6+8+10=24.
故答案为:24.
点评 此题主要考查了三角形中位线定理,关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
7.下列各式中,不能用平方差公式计算的是( )
| A. | (-x-y)(x-y) | B. | (x-y)(-x+y) | C. | (x+y)(-x+y) | D. | (-x+y)(-x-y) |
8.下列作图语句正确的是( )
| A. | 作线段AB,使α=AB | B. | 延长线段AB到C,使AC=BC | ||
| C. | 作∠AOB,使∠AOB=∠α | D. | 以O为圆心作弧 |
5.任意抛掷一枚硬币2次,两次都正面朝上的概率( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
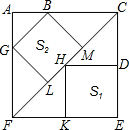 如图,边长为6的大正方形中有两个小正方形,两个小正方形的面积分别为S1、S2
如图,边长为6的大正方形中有两个小正方形,两个小正方形的面积分别为S1、S2