题目内容
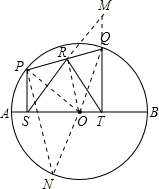
 已知AB是直径,弦PQ与AB不平行,R为PQ的中点,∠SRT=60°,PS⊥AB,TQ⊥AB,求
已知AB是直径,弦PQ与AB不平行,R为PQ的中点,∠SRT=60°,PS⊥AB,TQ⊥AB,求| PQ |
| AB |
考点:圆的综合题
专题:综合题
分析:连接OP,OR,OQ,延长TQ,交SR的延长线与点M,延长QO交圆O于点N,连接PN,可证:P、R、O、S四点共圆,则PQ:AB=PQ:NQ,即可求解.
解答:解:如图,连接OP、QO、OR、延长QO交⊙O于N,延长SR交TQ延长线于M,连接PN,
∵PS⊥AB,TQ⊥AB,
∴PS∥QT,
∴∠M=∠PSR,
在△PRS和△QRM中,
,
∴△PRS≌△QRM(AAS),
∴SR=RM,
又∵△MST为直角三角形,
∴SR=RT(直角三角形中斜边中线等于斜边一半),
∴SR=RT,
∵∠SRT=60°,
∴△SRT为正三角形,
∵R为PQ中点,
∴OR⊥PQ(垂径定理),
∴P、R、O、S四点共圆,
∴∠POR=∠PSR=30°,
同理,可证∠ROQ=∠RTQ=30°,
则∠POQ=60°,
∴PQ:AB=PQ:NQ=sin∠PNQ=sin30°=1:2,
即
的值为
.
∵PS⊥AB,TQ⊥AB,
∴PS∥QT,
∴∠M=∠PSR,

在△PRS和△QRM中,
|
∴△PRS≌△QRM(AAS),
∴SR=RM,
又∵△MST为直角三角形,
∴SR=RT(直角三角形中斜边中线等于斜边一半),
∴SR=RT,
∵∠SRT=60°,
∴△SRT为正三角形,
∵R为PQ中点,
∴OR⊥PQ(垂径定理),
∴P、R、O、S四点共圆,
∴∠POR=∠PSR=30°,
同理,可证∠ROQ=∠RTQ=30°,
则∠POQ=60°,
∴PQ:AB=PQ:NQ=sin∠PNQ=sin30°=1:2,
即
| PQ |
| AB |
| 1 |
| 2 |
点评:本题主要考查了求线段的比,利用圆周角定理把线段的比转化为三角函数的问题求解,难度较大,关键是能将所学的知识融会贯通.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
如果a=-2+
,那么1+
的值为( )
| 2 |
| 1 | ||
2+
|
A、-
| ||
B、
| ||
| C、2 | ||
D、2
|
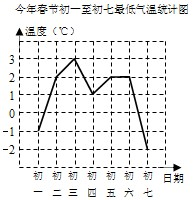 小华同学根据某地今年春节初一至初七的每天最低气温绘成了所示的折线统计图.关于这7天的每天最低气温的说法不正确的是( )
小华同学根据某地今年春节初一至初七的每天最低气温绘成了所示的折线统计图.关于这7天的每天最低气温的说法不正确的是( )| A、极差是5℃ |
| B、众数是2℃ |
| C、中位数是1℃ |
| D、平均数是1℃ |
 如图,AB∥EF∥CD,已知AC+BD=120,BC=50,EC+ED=96,求CF.
如图,AB∥EF∥CD,已知AC+BD=120,BC=50,EC+ED=96,求CF.