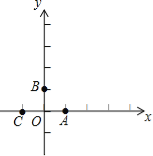Question

【题目】在平面直角坐标系中，抛物线y＝﹣x2﹣2x+3与x轴交于A，B两点（A在B的左侧），与y轴交于点C，顶点为D.

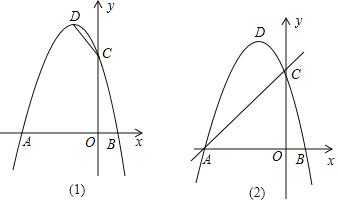
（1）求出点A，C，D的坐标；

（2）如图（1），在抛物线对称轴上找一点E，使得△CBE的周长最小，求点E的坐标；

（3）如图（2），作垂直x轴的直线，在第二象限交直线AC于点M，交抛物线于点N，求当MN有最大值时N点坐标？并求出MN最大值是多少？

Answer 1

【答案】（1）点A、C的坐标为（﹣3，0）、（0，3），顶点D（﹣1，4）；（2）点E（﹣1，2）；（3）MN有最大值，此时x＝﹣，故点N（﹣，）.

【解析】

（1）y=-x2-2x+3，令x=0，则y=3，令y=0，则x=-3或1，即可求解；

（2）作点C关于函数对称轴的对称点F，连接FB，交抛物线的对称轴于点E，点E为所求点，此时△CBE的周长=BC+EC+EB=BC+BE+EF=FB+BC，即可求解；

（3）先求出直线AC的解析式，设点N（x，-x2-2x+3），则点M（x，x+3），则MN=-x2-2x+3-x-3=-x2-3x，即可求解．

（1）y＝﹣x2﹣2x+3，令x＝0，则y＝3，令y＝0，则x＝﹣3或1，

故点A、B、C的坐标为（﹣3，0）、（1，0）、（0，3），

函数的对称轴为：x＝﹣1，故顶点D（﹣1，4）；

（2）作点C关于函数对称轴的对称点F，连接FB，交抛物线的对称轴于点E，点E为所求点，此时△CBE的周长＝BC+EC+EB＝BC+BE+EF＝FB+BC，

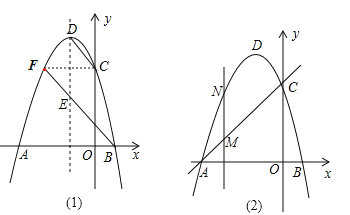
∵BC是常数，F、E、B共线，故此时△CBE的周长＝FB+BC最小，

∵（0，3），对称轴为：x＝﹣1，

∴点F（﹣2，3），

设BF的解析式为：y=kx+b，

将点B、F的坐标代入一次函数表达式得：

，解得：，

故直线BF的函数表达式为：y＝﹣x+1，

当x＝﹣1时，y＝2，故点E（﹣1，2）；

（3）将点A、C的坐标代入一次函数表达式，

设直线AC的解析式为：y=mx+n，

把A、C的坐标代入得

，解之得，

∴直线AC的函数表达式为：y＝x+3，

设点N（x，﹣x2﹣2x+3），则点M（x，x+3），

则MN＝﹣x2﹣2x+3﹣x﹣3＝﹣x2﹣3x，

∵﹣1＜0，故MN有最大值，此时x＝﹣，

故点N（﹣，）