题目内容
14.等腰三角形△ABC底角的余弦值是$\frac{2}{3}$,一边长为12,则等腰三角形的面积为32$\sqrt{5}$或18$\sqrt{5}$.分析 根据题意,分两种情况:(1)一条腰长为12时,根据等腰三角形△ABC底角的余弦值是$\frac{2}{3}$,以及等腰三角形的性质得到底和高,再根据三角形面积公式即可求解.(2底为12时,根据等腰三角形△ABC底角的余弦值是$\frac{2}{3}$,以及等腰三角形的性质得到高,再根据三角形面积公式即可求解.
解答 解:(1)一条腰长为12时,
∵等腰三角形△ABC底角的余弦值是$\frac{2}{3}$,
∴三角形的底=12×$\frac{2}{3}$×2=16,
∴三角形的高=$\sqrt{{12}^{2}{-(16÷2)}^{2}}$=4$\sqrt{5}$,
∴等腰三角形的面积=16×4$\sqrt{5}$÷2=32$\sqrt{5}$.
(2底为12时,
∵等腰三角形△ABC底角的余弦值是$\frac{2}{3}$,
∴三角形的高=12÷2÷$\frac{2}{3}$×$\sqrt{1{-(\frac{2}{3})}^{2}}$=3$\sqrt{5}$,
∴等腰三角形的面积=12×3$\sqrt{5}$÷2=18$\sqrt{5}$.
故答案为:32$\sqrt{5}$或18$\sqrt{5}$.
点评 此题主要考查了解直角三角形的方法和应用,以及等腰三角形的性质和应用,要熟练掌握,注意分两种情况讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9. 在锐角△ABC中,∠BAC=60°,BN、CM为高,P为BC的中点,连接MN、MP、NP,则结论:①NP=MP;②AN:AB=AM:AC;③BN=2AN;④当∠ABC=60°时,MN∥BC,一定正确的有( )
在锐角△ABC中,∠BAC=60°,BN、CM为高,P为BC的中点,连接MN、MP、NP,则结论:①NP=MP;②AN:AB=AM:AC;③BN=2AN;④当∠ABC=60°时,MN∥BC,一定正确的有( )
 在锐角△ABC中,∠BAC=60°,BN、CM为高,P为BC的中点,连接MN、MP、NP,则结论:①NP=MP;②AN:AB=AM:AC;③BN=2AN;④当∠ABC=60°时,MN∥BC,一定正确的有( )
在锐角△ABC中,∠BAC=60°,BN、CM为高,P为BC的中点,连接MN、MP、NP,则结论:①NP=MP;②AN:AB=AM:AC;③BN=2AN;④当∠ABC=60°时,MN∥BC,一定正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.一个几何体的主视图、左视图都是等边三角形,俯视图是一个圆,这个几何体是( )
| A. | 三棱柱 | B. | 三棱锥 | C. | 圆柱 | D. | 圆锥 |
 小明在荡秋千时,发观秋千在静止时,秋千离地面3dm(EF=3dm),荡起的水平距离为13dm(BC=13dm)时,离地面8dm(BD=8dm),求秋千的绳索AF的长.
小明在荡秋千时,发观秋千在静止时,秋千离地面3dm(EF=3dm),荡起的水平距离为13dm(BC=13dm)时,离地面8dm(BD=8dm),求秋千的绳索AF的长.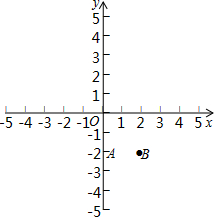 在如图的平面直角坐标系xOy中,抛物线y=2x2+bx+c经过点A(0,-2),B(2,-2).
在如图的平面直角坐标系xOy中,抛物线y=2x2+bx+c经过点A(0,-2),B(2,-2). 矩形ABCD中,AD=8cm,AB=6cm,动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动,E点运动到B点停止,F点继续运动,运动到点D停止.如图可得到矩形CFHE,设F点运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是如图中的( )
矩形ABCD中,AD=8cm,AB=6cm,动点E从点C开始沿边CB向点B以2cm/s的速度运动,动点F从点C同时出发沿边CD向点D以1cm/s的速度运动,E点运动到B点停止,F点继续运动,运动到点D停止.如图可得到矩形CFHE,设F点运动时间为x(单位:s),此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位:cm2),则y与x之间的函数关系用图象表示大致是如图中的( )


