题目内容
有一个Rt△ABC,∠A=90°,∠B=60°,AB=2,将它放在直角坐标系中,使斜边BC在x轴上,直角顶点A在反比例函数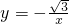 的图象上,则点C的横坐标________.
的图象上,则点C的横坐标________.
±4,±2
分析:本题可先设出A,B,C三点的坐标,再利用两点之间的线段公式,求出yA的值,再求出xA的值,即可由xA,xc的关系,求出C点的横坐标.
解答:设A(xA,yA),C(xc,0),B(xB,0),
B,C在x轴正半轴上时,
∵AB=2,∠B=60°,
∴BC=4,AC= ,
,
∴由两点之间的线段公式
得,(xA-xc)2+yA2=12 ①
(xA-xB)2+yA2=4 ②
xc-xB=4 ③
化简得,xc-xA=3,
将其代入①中得,yA=
∴xA=±1,
则xc=4或2,
同理可得,当B,C在x轴负半轴上时,
xc=-4或-2.
故答案为:±4,±2.
点评:本题将反比例函数与几何图形联系了起来,解答本题关键是要找出各量之间的关系.同时要注意BC即可在x轴负半轴上,也可在x轴正半轴上.
分析:本题可先设出A,B,C三点的坐标,再利用两点之间的线段公式,求出yA的值,再求出xA的值,即可由xA,xc的关系,求出C点的横坐标.
解答:设A(xA,yA),C(xc,0),B(xB,0),
B,C在x轴正半轴上时,
∵AB=2,∠B=60°,
∴BC=4,AC=
 ,
,∴由两点之间的线段公式
得,(xA-xc)2+yA2=12 ①
(xA-xB)2+yA2=4 ②
xc-xB=4 ③
化简得,xc-xA=3,
将其代入①中得,yA=

∴xA=±1,
则xc=4或2,
同理可得,当B,C在x轴负半轴上时,
xc=-4或-2.
故答案为:±4,±2.
点评:本题将反比例函数与几何图形联系了起来,解答本题关键是要找出各量之间的关系.同时要注意BC即可在x轴负半轴上,也可在x轴正半轴上.

练习册系列答案
相关题目
 相切,求m的值.
相切,求m的值. 如图,在12×6的网格中(每个小正方形的边长均为1个单位长),有一个Rt△ABC和一个半圆O(A、B、C、O均为格点),∠C=90°,半圆O的半径为2.将Rt△ABC沿AC方向向右平移m个单位,使其斜边恰好与半圆O相切,求m的值.
如图,在12×6的网格中(每个小正方形的边长均为1个单位长),有一个Rt△ABC和一个半圆O(A、B、C、O均为格点),∠C=90°,半圆O的半径为2.将Rt△ABC沿AC方向向右平移m个单位,使其斜边恰好与半圆O相切,求m的值. 有一个Rt△ABC,∠A=90°,∠B=60°,AB=1,将它放在如图直角坐标系中,使斜边BC在x轴上,直角顶点A在反比例函数y=-
有一个Rt△ABC,∠A=90°,∠B=60°,AB=1,将它放在如图直角坐标系中,使斜边BC在x轴上,直角顶点A在反比例函数y=-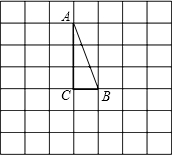 在如图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°.现将Rt△ABC绕点B顺时针旋转90°后所得到的Rt△A′BC'.
在如图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=90°.现将Rt△ABC绕点B顺时针旋转90°后所得到的Rt△A′BC'.