题目内容
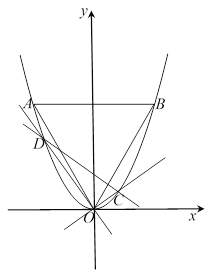
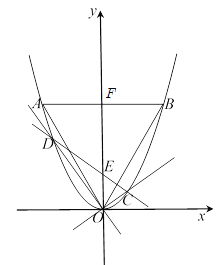
【题目】如图,等边三角形![]() 的边长为
的边长为![]() ,且其三个顶点均在抛物线
,且其三个顶点均在抛物线![]() 上.
上.
(1)求抛物线的解析式;
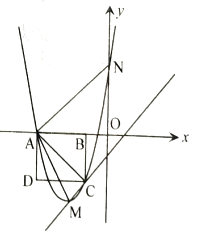
(2)若过原点![]() 的直线
的直线![]() 与直线
与直线![]() 分别交抛物线
分别交抛物线![]() 于点
于点![]() 、
、![]() ,
,
①当![]() 时,试求
时,试求![]() 的面积;
的面积;
②试证明:不论实数![]() 取何值,直线
取何值,直线![]() 总是经过一定点.
总是经过一定点.
【答案】(1)![]() ;(2)①20;②详见解析
;(2)①20;②详见解析
【解析】
(1)如图,由题意可得OB=![]() ,∠ABO=60°,然后在Rt△BOF中,利用解直角三角形的知识求出BF和OF的长,进而可得点B坐标,然后代入抛物线的解析式即可求出结果;
,∠ABO=60°,然后在Rt△BOF中,利用解直角三角形的知识求出BF和OF的长,进而可得点B坐标,然后代入抛物线的解析式即可求出结果;
(2)①先解方程组求出点C、D的坐标,再利用待定系数法求出直线CD的解析式,然后即可求出直线![]() 与
与![]() 轴的交点
轴的交点![]() ,再根据
,再根据![]() 计算即可;
计算即可;
②先解方程组求出点C、D的坐标,再利用待定系数法求出直线CD的解析式,然后即可求出直线![]() 与
与![]() 轴的交点,进而可得结论.
轴的交点,进而可得结论.
解:(1)如图,![]() 等边△
等边△![]() 的边长为
的边长为![]() ,
,
∴OB=![]() ,∠ABO=60°,
,∠ABO=60°,
则在Rt△BOF中,BF=4,![]() ,
,
![]() ,
,
又点![]() 在抛物线
在抛物线![]() 上,
上,
![]()
![]() ,解得:
,解得:![]() ,
,
故所求的解析式为![]() ;
;
(2)①解方程组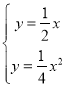 ,得
,得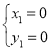 ,
,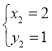 ,∴
,∴![]() ,
,
解方程组 ,得
,得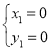 ,
, ,∴
,∴![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
![]() ,解得:
,解得: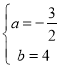 ,
,
所以直线![]() 的解析式为
的解析式为![]() ,
,
设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,则
,则![]() ,如图,
,如图,

∵![]() ,
,![]() ,
,
![]() ;
;
②解方程组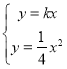 ,得
,得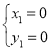 ,
,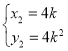 ,∴
,∴![]() ,
,
解方程组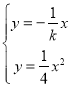 ,得
,得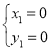 ,
,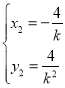 ,∴
,∴![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
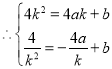 ,解得:
,解得: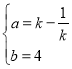 ,
,
所以直线![]() 的解析式为
的解析式为![]() ,
,
所以不论实数![]() 取何值,直线
取何值,直线![]() 总过定点
总过定点![]() .
.

练习册系列答案
相关题目