题目内容
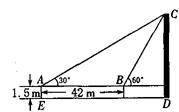
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M从点C出发,以每秒1cm的速度沿CA向终点A移动,同时动点P从点A出发,以每秒2cm的速度沿AB向终点B移动,连接PM,设移动时间为t(s)(0<t<2.5).
(1)当AP=AM时,求t的值.
(2)设四边形BPMC的面积为 (cm²),求y与t之间的函数关系式;
(cm²),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形BPMC的面积是Rt△ABC面积的 ?若存在,求出相应t的值,若不存在,说明理由;
?若存在,求出相应t的值,若不存在,说明理由;
(4)是否存在某一时刻t,使以M,P,A为顶点的三角形与△ABC相似?若存在,求出相应t的值;若不存在,说明理由.
解:(1)如图,
 ∵在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.
∵在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.
∴根据勾股定理,得AB= =5cm.
=5cm.
AM=4-t,AP=2t
当AP=AM时,则
4-t= 2t, ∴
当 时, AP=AM
时, AP=AM
(2)过点P作PH⊥AC于点H,则PH∥BC,
 ∴
∴ ,
,
即
∴PH= .
.

∴ =6-(
=6-( )
)
=


练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 _____________.
_____________. ,则
,则 ;②
;② ;
; ,则
,则 .
.
 ≈1.7)
≈1.7)
 ∠B︰∠C=1︰1︰2,则=( )
∠B︰∠C=1︰1︰2,则=( ) ,△ABC的周长为6
,△ABC的周长为6 0,那么△ABC的面积为( )
0,那么△ABC的面积为( ) 据:
据: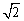 ≈1.4,
≈1.4,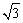 ≈1.7).
≈1.7).