题目内容
已知：如图，锐角△ABC的两条高CD、BE相交于点O，且OB=OC
1.求证：△ABC是等腰三角形
2.连结AO，判断AO与BC的位置关系，并说明理由.
1.见解析
2.点O在∠BAC的角平分线上
解析:(1)∵OB=OC，
∴∠OBC=∠OCB，
∵锐角△ABC的两条高BD、CE相交于点O，
∴∠BEC=∠BDC=90°，
∵∠BEC+∠BCE+∠ABC=∠BDC+∠DBC+∠ACB=180°，
∴∠ABC=∠ACB，
∴AB=AC，
∴△ABC是等腰三角形；
（2）点O在∠BAC的角平分线上．
理由：连接AO并延长交BC于F，
∵AB=AC，OB=OC，
又∵OA=OA，
∴△AOB≌△AOC．
∴∠BAF=∠CAF，
∴点O在∠BAC的角平分线上
练习册系列答案
三点一测快乐周计划系列答案
相关题目
10、已知：如图，锐角△ABC的两条高BD、CE相交于点O，且OB=OC．
15、已知，如图，锐角△ABC中，AD⊥BC于D，H为垂心（三角形三条高线的交点）；在AD上有一点P，且∠BPC为直角．
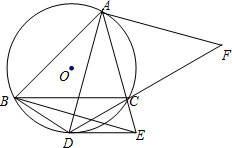点D的切线DE交AC的延长线于点E，且DE∥BC；连接AD、BD、BE，AD的垂线AF与DC的延长线交于点F．
已知：如图，锐角△ABC内接于⊙O，∠ABC=45°；点D是
已知：如图，锐角△ABC的两条高BD、CE相交于点O，且OB=OC．