题目内容
O为△ABC内一点，AO、BO、CO及其延长线把△ABC分成六个小三角形，它们的面积如图所示，则S△ABC=
- A.292
- B.315
- C.322
- D.357
B
分析：利用已知面积求出AO与DO之比即三角形ABO和三角形BDO的面积之比，得出关于x，y的方程．同理求出BO与OE之比，得出关于x，y的方程．两个方程联立解出x，y的值，再求三角形ABC的面积．
解答：∵
，即
，
又∵
，即
，
∴
，
解之得
，
∴S△ABC=84+40+30+35+70+56=315．
故选B．
点评：考查了三角形面积的计算．关键掌握等高的两个三角形面积之比等于底边边长之比．
分析：利用已知面积求出AO与DO之比即三角形ABO和三角形BDO的面积之比，得出关于x，y的方程．同理求出BO与OE之比，得出关于x，y的方程．两个方程联立解出x，y的值，再求三角形ABC的面积．
解答：∵
，即，又∵
，即，∴
，解之得
，∴S△ABC=84+40+30+35+70+56=315．
故选B．
点评：考查了三角形面积的计算．关键掌握等高的两个三角形面积之比等于底边边长之比．
练习册系列答案
相关题目
如图，△ABC中，AC=BC=5，∠ACB=80°，O为△ABC内一点，∠OAB=10°，∠OBA=30°，则线段AO的长是多少？
如图，在△ABC中，AB=AC，∠BAC=80°，O为△ABC内一点，且∠OBC=10°，∠OCA=20°，求∠BAO的度数．
14、如图，已知△ABC中，∠BAC=120°，P为△ABC内一点．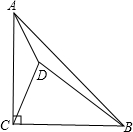
如图，在Rt△ABC中，∠ACB=90°，AC=BC，点D为△ABC内一点，AD=1，而DC、DB的长是关于x的方程x2-kx+6=0的两个实数根x1，x2（DC＜DB）并且
如图，△ABC中，AB=AC，∠A=50°，P为△ABC内一点，∠PBC=∠PCA，求∠BPC的值．